第二章 随机变量及其分布

知识结构网络图
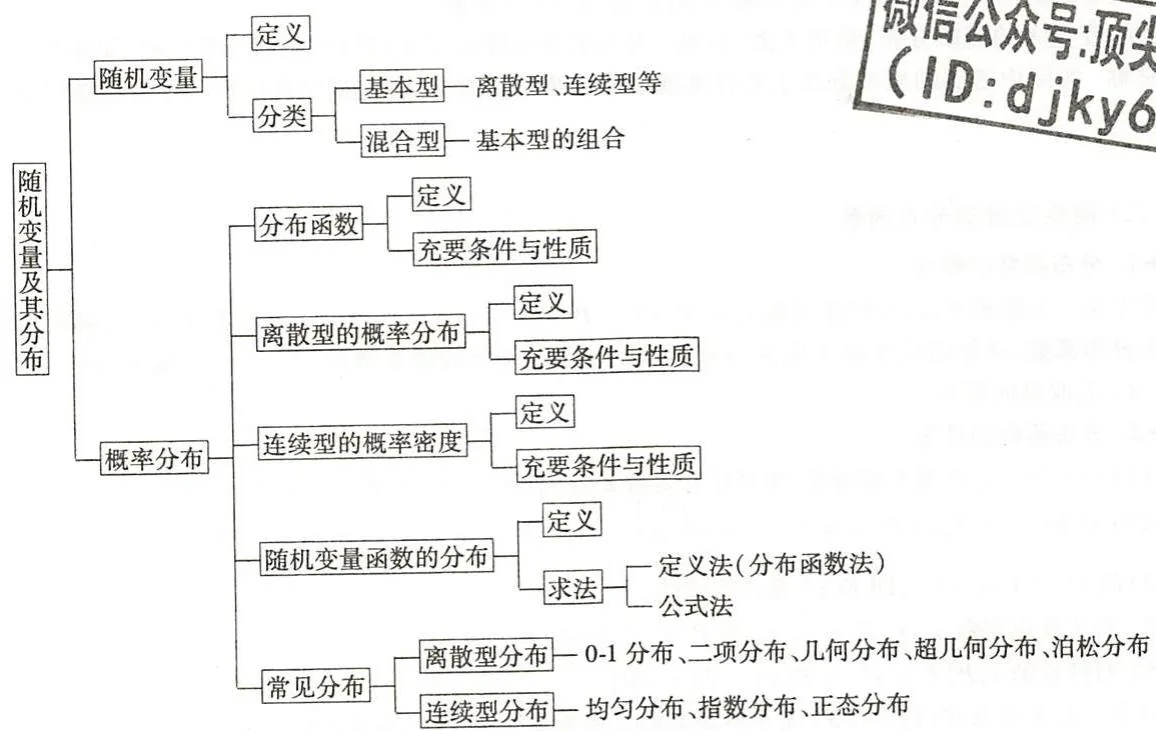

内容概要与重难点提示
随机变量是概率论与数理统计所要研究的基本对象,它是定义在样本空间上具有某种可测性的实值函数。我们关心的是它取哪些值以及以怎样的概率取这些值,而分布函数则完整地描述了随机变量取值的统计规律,又由于分布函数有良好的分析性质,因此它是研究随机变量的重要工具。
离散型与连续型随机变量是最重要的两类随机变量,它们因取值范围的不同,在描述与处理方法上亦有很大差异。考生要对比其异同,理解离散型随机变量的概率分布与连续型随机变量的概率密度以及它们与分布函数间的关系。
在实际应用与理论研究中都很重要的几种分布,即所谓常见分布,考生要掌握其分布规律及其应用,并理解分布参数的概率意义,常见分布主要是0-1分布、二项分布、几何分布、超几何分布、泊松分布、均匀分布、指数分布与正态分布。
随机变量函数的分布,主要难点是求连续型随机变量函数的分布,其最基本的方法是分布函数法。
练习题
例题1
题目内容
设随机变量 (X\( 服从参数为 \(\lambda = 2\) 的泊松分布,即 (X \sim P(2)\(。求 \(P(X = 3)\) 和 (P(X \leq 2)$。
题目解答
泊松分布的概率分布为 (P(X = k) = \frac{\lambda^k e^{-\lambda}}{k!}\(,其中 \(\lambda = 2\)。
- (P(X = 3) = \frac{2^3 e^{-2}}{3!} = \frac{8 \cdot e^{-2}}{6} \approx \frac{8 \cdot 0.1353}{6} \approx 0.1804$。
- (P(X \leq 2) = P(X = 0) + P(X = 1) + P(X = 2)\(:
\(P(X = 0) = \frac{2^0 e^{-2}}{0!} = e^{-2} \approx 0.1353\),
(P(X = 1) = \frac{2^1 e^{-2}}{1!} = 2e^{-2} \approx 0.2707\(, \(P(X = 2) = \frac{2^2 e^{-2}}{2!} = \frac{4 \cdot e^{-2}}{2} \approx 2 \cdot 0.1353 = 0.2706\),
所以 (P(X \leq 2) \approx 0.1353 + 0.2707 + 0.2706 = 0.6766$。
例题2
题目内容
设随机变量 (X\( 服从区间 \([0, 2]\) 上的均匀分布,即 (X \sim U(0, 2)\(。求 \(X\) 的分布函数 (F(x)\( 和概率密度函数 \(f(x)\),并计算 (P(0.5 < X < 1.5)$。
题目解答
均匀分布的概率密度函数为 (f(x) = \frac{1}{b-a}\( 在区间 \([a, b]\) 上,这里 (a = 0, b = 2\(,所以 \(f(x) = \frac{1}{2}\) 对于 (x \in [0, 2]\(,否则为 0。
分布函数 \(F(x) = \int_{-\infty}^{x} f(t) \, dt\):
- 若 (x < 0\(,则 \(F(x) = 0\);
- 若 (0 \leq x \leq 2\(,则 \(F(x) = \int_{0}^{x} \frac{1}{2} \, dt = \frac{x}{2}\);
- 若 (x > 2\(,则 \(F(x) = 1\)。
(P(0.5 < X < 1.5) = F(1.5) - F(0.5) = \frac{1.5}{2} - \frac{0.5}{2} = 0.75 - 0.25 = 0.5$。
例题3
题目内容
设随机变量 (X\( 服从参数为 \(\lambda = 0.5\) 的指数分布,即 (X \sim Exp(0.5)\(。求 \(X\) 的分布函数 (F(x)\( 和概率密度函数 \(f(x)\),并计算 (P(X > 2)$。
题目解答
指数分布的概率密度函数为 (f(x) = \lambda e^{-\lambda x}\( 对于 \(x \geq 0\),这里 (\lambda = 0.5\(,所以 \(f(x) = 0.5 e^{-0.5x}\)。
分布函数 (F(x) = 1 - e^{-\lambda x}\( 对于 \(x \geq 0\),所以 (F(x) = 1 - e^{-0.5x}\(。
\(P(X > 2) = 1 - F(2) = 1 - (1 - e^{-0.5 \cdot 2}) = e^{-1} \approx 0.3679\)。
例题4
题目内容
设随机变量 (X\( 的概率密度函数为 \(f(x) = \frac{1}{2} e^{-|x|}\)(双指数分布)。求 (X\( 的分布函数 \(F(x)\),并验证其满足分布函数的性质。
题目解答
由于 (f(x) = \frac{1}{2} e^{-|x|}$,需分段计算分布函数:
- 对于 (x < 0\(,\(F(x) = \int_{-\infty}^{x} \frac{1}{2} e^{t} \, dt = \frac{1}{2} e^{x}\)(因为 (e^{-|t|} = e^{t}\( 当 \(t < 0\))。
- 对于 (x \geq 0\(,\(F(x) = \int_{-\infty}^{0} \frac{1}{2} e^{t} \, dt + \int_{0}^{x} \frac{1}{2} e^{-t} \, dt = \frac{1}{2} + \frac{1}{2} (1 - e^{-x}) = 1 - \frac{1}{2} e^{-x}\)。
验证分布函数性质:
- (F(x)\( 非减:在 \(x < 0\) 时导数为 (\frac{1}{2} e^{x} > 0\(,在 \(x \geq 0\) 时导数为 (\frac{1}{2} e^{-x} > 0$。
- (\lim_{x \to -\infty} F(x) = 0\(,\(\lim_{x \to \infty} F(x) = 1\)。
- (F(x)\( 右连续:在 \(x = 0\) 处,左极限为 (\frac{1}{2}\(,右值为 \(1 - \frac{1}{2} = \frac{1}{2}\),连续。
例题5
题目内容
设随机变量 (X \sim N(1, 4)\((正态分布,均值为 1,方差为 4)。求 \(P(0 < X < 2)\),并使用标准正态分布表计算。
题目解答
若 (X \sim N(\mu, \sigma^2)\(,则 \(Z = \frac{X - \mu}{\sigma} \sim N(0, 1)\)。这里 (\mu = 1, \sigma = 2\(。
\(P(0 < X < 2) = P\left(\frac{0-1}{2} < Z < \frac{2-1}{2}\right) = P(-0.5 < Z < 0.5)\)。
由标准正态分布对称性,(P(-0.5 < Z < 0.5) = 2P(0 < Z < 0.5)\(。查表得 \(P(0 < Z < 0.5) \approx 0.1915\),
所以 (P(0 < X < 2) \approx 2 \cdot 0.1915 = 0.3830$。
例题6
题目内容
设随机变量 (X\( 服从二项分布 \(B(5, 0.3)\)。求 (X\( 的概率分布,并计算 \(E(X)\) 和 (Var(X)$。
题目解答
二项分布 (B(n, p)\( 的概率分布为 \(P(X = k) = \binom{n}{k} p^k (1-p)^{n-k}\),这里 (n = 5, p = 0.3$。
- (P(X = 0) = \binom{5}{0} (0.3)^0 (0.7)^5 \approx 0.1681\(,
\(P(X = 1) = \binom{5}{1} (0.3)^1 (0.7)^4 \approx 0.3601\),
(P(X = 2) = \binom{5}{2} (0.3)^2 (0.7)^3 \approx 0.3087\(, \(P(X = 3) = \binom{5}{3} (0.3)^3 (0.7)^2 \approx 0.1323\),
(P(X = 4) = \binom{5}{4} (0.3)^4 (0.7)^1 \approx 0.0284\(, \(P(X = 5) = \binom{5}{5} (0.3)^5 (0.7)^0 \approx 0.0024\)。
期望 (E(X) = np = 5 \cdot 0.3 = 1.5\(,方差 \(Var(X) = np(1-p) = 5 \cdot 0.3 \cdot 0.7 = 1.05\)。