六、多元函数积分学的物理应用
利用各类积分可以解决相应类型的物体的质量、质心、形心、转动惯量,对质点的引力及功与流量等问题。解决这类问题的基本步骤是:
第一步,首先知道 \(n\) 个质点组的质点系的质量、质心、惯动惯量、对质点的引力等;
第二步,把相应的物体分割,近似看成 \(n\) 个质点组成的质点系,求出这些量的近似值;
第三步,无限细分,令 \(n\to \infty\) 就得到这些量的相应的积分表示。
【注】 上述步骤可用微元法代替。
(一)质量、质心、形心与转动惯量
-
在空间直角坐标系 \(Oxyz\) 中,\(n\) 个质点组成的质点组 \(M_{i}(x_{i},y_{i},z_{i})\),质量 \(m_i,i = 1,2,\dots ,n\),则质点组的
(1) 质心 \((\bar{x}, \bar{y}, \bar{z}) = \left(\sum_{i=1}^{n} x_{i} m_{i}, \sum_{i=1}^{n} y_{i} m_{i}, \sum_{i=1}^{n} z_{i} m_{i}\right) / \sum_{i=1}^{n} m_{i}\);
(2) 关于直线 \(L\) 与点 \(P\) 的转动惯量分别为 \(I_{L} = \sum_{i=1}^{n} r_{i}^{2} m_{i}\),\(I_{P} = \sum_{i=1}^{n} d_{i}^{2} m_{i}\),其中 \(r_{i}, d_{i}\) 分别是点 \(M_{i}\) 到直线 \(L\) 与点 \(P\) 的距离。 -
在空间直角坐标系 \(Oxyz\) 中,物体占据空间区域 \(\Omega\),体密度为 \(\rho(x,y,z)\),则
(1)质量 \(M = \iiint_{\Omega} \rho(x, y, z) \, \mathrm{d}V\);
(2)质心 \((\bar{x},\bar{y},\bar{z}) = \Big(\iiint_{\Omega}x\rho (x,y,z)\mathrm{d}V,\iiint_{\Omega}y\rho (x,y,z)\mathrm{d}V,\iiint_{\Omega}z\rho (x,y,z)\mathrm{d}V\Big) / \iiint_{\Omega}\rho \mathrm{d}V\),\((\bar{x},\bar{y},\bar{z})\) 也叫作空间区域 \(\Omega\) 的形心;
(3)关于 \(x, y, z\) 轴及原点的转动惯量分别为
\[I _ {x} = \iiint_ {\Omega} (y ^ {2} + z ^ {2}) \rho (x, y, z) \mathrm {d} V, \quad I _ {y} = \iiint_ {\Omega} (x ^ {2} + z ^ {2}) \rho (x, y, z) \mathrm {d} V,\] \[I _ {z} = \iiint_ {\Omega} (x ^ {2} + y ^ {2}) \rho (x, y, z) \mathrm {d} V, \quad I _ {o} = \iiint_ {\Omega} (x ^ {2} + y ^ {2} + z ^ {2}) \rho (x, y, z) \mathrm {d} V.\] -
对于平面薄片,若知其面密度,或曲面形物体知其面密度,或曲线形物体知其线密度,均可类似地得到质量、质心及转动惯量等相应的积分表达式。这时物体的质心也是相应的几何图形的形心。
(二)引力计算
-
质点 \(M_0(x_0, y_0, z_0), M_i(x_i, y_i, z_i)\) 的质量分别为 \(m_0\) 与 \(m_i\),则 \(M_i\) 对 \(M_0\) 的引力为
\[\boldsymbol {F} = \frac {k m _ {0} m _ {i}}{r _ {i} ^ {3}} \boldsymbol {r} _ {i},\]其中 \(k\) 为引力常数,\(\pmb{r}_i = \overline{\pmb{M}_0\pmb{M}_i} = (x_i - x_0,y_i - y_0,z_i - z_0)\)
\[r _ {i} = \left| r _ {i} \right| = \left[ \left(x _ {i} - x _ {0}\right) ^ {2} + \left(y _ {i} - y _ {0}\right) ^ {2} + \left(z _ {i} - z _ {0}\right) ^ {2} \right] ^ {\frac {1}{2}}.\] -
空间曲线 \(L\) 对 \(L\) 外点 \(M_0(x_0,y_0,z_0)\) 处质量为 \(m_0\) 的质点的引力为
\[\boldsymbol {F} = \int_ {L} k m _ {0} \rho (x, y, z) \frac {1}{r ^ {3}} (x - x _ {0}, y - y _ {0}, z - z _ {0}) d s,\]其中 \(\rho (x,y,z)\) 是 \(L\) 的线密度。
-
空间曲面 \(S\) 或空间区域 \(\Omega\) 对其外一点 \(M_0(x_0,y_0,z_0)\) 处质量为 \(m_0\) 的质点的引力分别有类似的曲面积分与三重积分表达式。(有关例子参见本章题型训练七之题16。)
(三)功的计算
-
点 \(M\) 在常力 \(F = (P, Q, R)\) 作用下由 \(A(x_A, y_A, z_A)\) 沿直线运动到 \(B(x_B, y_B, z_B)\),则力 \(F\) 做的功为
\[W = F \cdot \overrightarrow {A B} = P \cdot \left(x _ {B} - x _ {A}\right) + Q \cdot \left(y _ {B} - y _ {A}\right) + R \left(z _ {B} - z _ {A}\right).\] -
质点 \(M\) 在变力 \(F(x, y, z) = (P(x, y, z), Q(x, y, z), R(x, y, z))\) 作用下由 \(A\) 点沿曲线 \(C\) 运动到 \(B\) 点,则 \(F\) 对质点 \(M\) 做的功为
\[W = \int_ {\widehat {A B}} P \mathrm {d} x + Q \mathrm {d} y + R \mathrm {d} z.\] -
质点 \(M\) 在平面力 \(F(x,y) = (P(x,y),Q(x,y))\) 的作用下由 \(A\) 点沿平面曲线 \(C\) 运动到 \(B\) 点,则 \(\pmb{F}\) 对质点 \(M\) 做的功为
\[W = \int_ {\widehat {A B}} P \mathrm {d} x + Q \mathrm {d} y.\]
(四)流量计算
-
流体在空间流动,流速 \(v\) 为常向量,则单位时间内流过定向平面上区域 \(D\) 的流体体积(即体积流量,简称流量)为
\[q = | v | \cos \theta \cdot S = v \cdot n S,\]其中 \(\pmb{n}\) 是定向平面的单位法向量,\(\theta\) 是 \(\pmb{\nu}\) 与 \(\pmb{n}\) 的夹角,\(S\) 是 \(D\) 的面积(图9.38)。
-
流体在空间流动,流速为
\[v (x, y, z) = (P (x, y, z), Q (x, y, z), R (x, y, z)),\]则流体流过定向曲面 \(S\) 的流量为
\[\begin{array}{l} q = \iint_ {S} \boldsymbol {v} \cdot \boldsymbol {n} d S = \iint_ {S} (P \cos \alpha + Q \cos \beta + R \cos \gamma) d S \\ = \iint_ {S} P \mathrm {d} y \mathrm {d} z + Q \mathrm {d} z \mathrm {d} x + R \mathrm {d} x \mathrm {d} y, \\ \end{array}\]其中 \(\pmb{n}\) 是曲面 \(S\) 的单位向量,且 \(\pmb {n} = (\cos \alpha ,\cos \beta ,\cos \gamma)\)
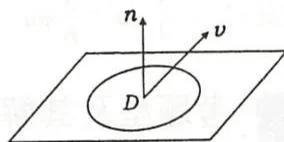
图9.38
例题
例9.32
记 \(I_{l}\) 为物体对 \(l\) 轴的转动惯量,\(I_{i}\) 为对平行于 \(l\) 轴并通过物体质心的轴 \(l\) 的转动惯量。\(d\) 为两轴间的距离,\(M\) 为物体的质量,证明:\(I_{l} = I_{\bar{l}} + Md^{2}\)
【证明】取 \(l\) 轴为 \(Oz\) 轴,按右手系建立直角坐标系(如图9.39)。设物体占有空间区域 \(\Omega\),物体的质心坐标为 \((\bar{x},\bar{y},\bar{z})\),则由已知条件有
\[\bar {x} ^ {2} + \bar {y} ^ {2} = d ^ {2}, \quad \bar {x} = \frac {1}{M} \iiint_ {\Omega} \rho x \mathrm {d} V, \quad \bar {y} = \frac {1}{M} \iiint_ {\Omega} \rho y \mathrm {d} V,\]其中 \(\rho\) 为物体的体密度。
物体对 \(\bar{l}\) 的转动惯量为
\[\begin{array}{l} I _ {\bar {i}} = \iiint_ {\Omega} \rho \left[ (x - \bar {x}) ^ {2} + (y - \bar {y}) ^ {2} \right] d V \\ = \iiint_ {\Omega} \rho \left(x ^ {2} + y ^ {2}\right) d V + \iiint_ {\Omega} \rho \left(\vec {x} ^ {2} + \vec {y} ^ {2}\right) d V - 2 \iiint_ {\Omega} \left(x \bar {x} + y \bar {y}\right) \rho d V \\ = I _ {l} + d ^ {2} M - 2 \bar {x} \iiint_ {\Omega} x \rho \mathrm {d} V - 2 \bar {y} \iiint_ {\Omega} y \rho \mathrm {d} V = I _ {l} + d ^ {2} M - 2 M (\bar {x} ^ {2} + \bar {y} ^ {2}) = I _ {l} - d ^ {2} M, \\ \end{array}\]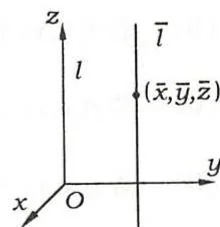
图9.39
即 \(I_{l} = I_{\hat{l}} + Md^{2}\)
例9.33
设一均匀物体由两曲面 \(x^{2} + y^{2} = az, z = 2a - \sqrt{x^{2} + y^{2}} (a > 0)\) 所围成,求此物体质心。
【解】根据质量分布的均匀性以及图形关于 \(z\) 轴的对称性可知,质心的坐标为 \((0,0,z^{*})\),由质心坐标的计算公式得
\[z ^ {*} = \frac {\iiint_ {\Omega} z \rho \mathrm {d} V}{\iiint_ {\Omega} \rho \mathrm {d} V} = \frac {\iiint_ {\Omega} z \mathrm {d} V}{\iiint_ {\Omega} \mathrm {d} V},\]其中 \(\varOmega\) 是该物体占据的空间区域,\(\rho\) 是物体的体密度,它为常数。
在【例9.30】中已经求得 \(\iiint_{\Omega} \mathrm{d}V = \frac{5}{6}\pi a^3\)。用先二后一的顺序求三重积分:
\[\begin{array}{l} \iiint_ {\Omega} z \mathrm {d} V = \int_ {0} ^ {2 a} \left(\iint_ {D (z)} z \mathrm {d} x \mathrm {d} y\right) \mathrm {d} z = \int_ {0} ^ {a} z \cdot \pi a z \mathrm {d} z + \int_ {a} ^ {2 a} z \pi (2 a - z) ^ {2} \mathrm {d} z \\ = \pi a \cdot \frac {1}{3} z ^ {3} \left| _ {0} ^ {a} + \pi \int_ {a} ^ {2 a} (z - 2 a) ^ {3} d z + \pi \int_ {a} ^ {2 a} 2 a (z - 2 a) ^ {2} d z \right. \\ = \frac {1}{3} \pi a ^ {4} + \frac {\pi}{4} (z - 2 a) ^ {4} \left| _ {a} ^ {2 a} + \frac {2 \pi a}{3} (z - 2 a) ^ {3} \right| _ {a} ^ {2 a} \\ = \frac {1}{3} \pi a ^ {4} - \frac {\pi}{4} a ^ {4} + \frac {2}{3} \pi a ^ {4} = \frac {3}{4} \pi a ^ {4}, \\ \end{array}\]因此 \(z^{*} = \frac{3}{4}\pi a^{4} / \frac{5}{6}\pi a^{3} = \frac{9}{10} a\),所求质心为 \(\left(0,0,\frac{9}{10} a\right)\)
练习题
例题1
计算由曲面 \(z = x^2 + y^2\) 和 \(z = 4\) 所围成的均匀物体的质心坐标。假设物体密度为常数 \(\rho\)。
题目解答
由于物体密度均匀且图形关于 \(z\)-轴对称,质心坐标为 \((0, 0, \bar{z})\)。
质量 \(M = \iiint_{\Omega} \rho \, dV\),
\(\bar{z} = \frac{1}{M} \iiint_{\Omega} z \rho \, dV\)。
在柱坐标下,区域 \(\Omega\) 由 \(0 \leq \theta \leq 2\pi\),\(0 \leq r \leq 2\),\(r^2 \leq z \leq 4\) 描述。
计算:
因此,
\[\bar{z} = \frac{(64\pi/3)\rho}{8\pi\rho} = \frac{8}{3}.\]质心为 \((0, 0, \frac{8}{3})\)。
例题2
设一均匀物体由曲面 \(z = \sqrt{x^2 + y^2}\) 和 \(z = 1\) 所围成,求该物体关于 \(z\)-轴的转动惯量 \(I_z\)。
题目解答
密度 \(\rho\) 为常数。在柱坐标下,区域 \(\Omega\) 由 \(0 \leq \theta \leq 2\pi\),\(0 \leq r \leq 1\),\(r \leq z \leq 1\) 描述。
转动惯量 \(I_z = \iiint_{\Omega} (x^2 + y^2) \rho \, dV = \rho \iiint_{\Omega} r^2 \, dV\)。
计算:
例题3
设有一平面薄片,形状为区域 \(D: x^2 + y^2 \leq 1, y \geq 0\),面密度为 \(\mu(x,y) = y\)。求该薄片的质量和质心坐标。
题目解答
在极坐标下,\(x = r\cos\theta, y = r\sin\theta\),区域 \(D\) 对应 \(0 \leq \theta \leq \pi\),\(0 \leq r \leq 1\)。
质量:
质心:
\[\bar{x} = \frac{1}{M} \iint_D x \mu \, dA = \frac{3}{2} \int_0^{\pi} \int_0^1 (r\cos\theta)(r\sin\theta) r \, dr d\theta = \frac{3}{2} \int_0^{\pi} \cos\theta\sin\theta \, d\theta \int_0^1 r^3 \, dr.\] \[\int_0^{\pi} \cos\theta\sin\theta \, d\theta = \frac{1}{2} \int_0^{\pi} \sin 2\theta \, d\theta = \frac{1}{2} \left[-\frac{\cos 2\theta}{2}\right]_0^{\pi} = 0 \quad \Rightarrow \bar{x} = 0.\] \[\bar{y} = \frac{1}{M} \iint_D y \mu \, dA = \frac{3}{2} \int_0^{\pi} \int_0^1 (r\sin\theta)(r\sin\theta) r \, dr d\theta = \frac{3}{2} \int_0^{\pi} \sin^2\theta \, d\theta \int_0^1 r^3 \, dr.\] \[\int_0^{\pi} \sin^2\theta \, d\theta = \frac{\pi}{2}, \quad \int_0^1 r^3 \, dr = \frac{1}{4} \quad \Rightarrow \bar{y} = \frac{3}{2} \cdot \frac{\pi}{2} \cdot \frac{1}{4} = \frac{3\pi}{16}.\]质心为 \((0, \frac{3\pi}{16})\)。
例题4
设力场 \(\mathbf{F} = (y, -x, z)\),求质点沿曲线 \(C: \mathbf{r}(t) = (\cos t, \sin t, t)\),从 \(t = 0\) 到 \(t = 2\pi\) 运动时,力 \(\mathbf{F}\) 所做的功。
题目解答
功 \(W = \int_C \mathbf{F} \cdot d\mathbf{r} = \int_C y \, dx - x \, dy + z \, dz\)。
参数化:\(x = \cos t, y = \sin t, z = t\),则 \(dx = -\sin t \, dt, dy = \cos t \, dt, dz = dt\)。
代入: