# 八、一元函数积分学的物理应用
## (一)液体的静压力
在液面下深度为 $h$ 处,由液体重量产生的压强等于它的深度 $h$ 与液体比重 $\gamma$ 的乘积:$p = \gamma h$。并且同一点的压强在各个方向都是相等的。
设一薄板垂直放在均匀的静止液体中,如图3.16,则液体对薄板的侧压力
$$
P = \int_{a}^{b} \gamma x f(x) dx,
$$
其中 $\gamma$ 为液体的密度,$f(x)$ 在 $[a, b]$ 连续($[x, x + \mathrm{d}x]$ 对应的小条薄板所受的侧压力 $\mathrm{d}P = \gamma x f(x) \mathrm{d}x$)。
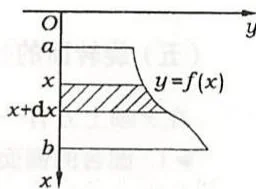
图3.16
【例3.30】有一椭圆形薄板,长半轴为 $a$,短半轴为 $b$,薄板垂直立于水中,而其短半轴与水面相齐,求水对薄板的侧压力。
【解法一】取坐标系如图3.17所示,椭圆方程为 $\frac{x^2}{a^2} +\frac{y^2}{b^2} = 1$。分割区间 $[0,a]$,在小区间 $[x,x+dx]$ 对应的小横条薄板上,水对它的压力
$$
\mathrm{d}P = \text{压强} \times \text{面积} = \gamma x \cdot 2y \mathrm{d}x = \gamma x \frac{2b}{a} \sqrt{a^{2} - x^{2}} \mathrm{d}x,
$$
其中 $\gamma$ 为水的比重。于是从0到 $a$ 积分便得到椭圆形薄板所受的压力
$$
\begin{aligned}
P &= \int_{0}^{a} \frac{2b\gamma}{a} x \sqrt{a^{2} - x^{2}} dx \\
&= -\frac{b\gamma}{a} \frac{2}{3} (a^{2} - x^{2})^{\frac{1}{3}} \Bigg|_{0}^{a} \\
&= \frac{2}{3} \gamma a^{2} b.
\end{aligned}
$$

图3.17
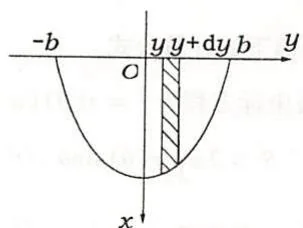
图3.18
【解法二】分割区间 $[-b, b]$,在小区间 $[y, y + \mathrm{d}y]$ 对应的小竖条薄板上,水对它的压力(如图3.18所示)
$$
\mathrm{d}P = \text{中心处的压强} \times \text{面积} = \gamma \cdot \frac{x}{2} x\mathrm{d}y = \frac{\gamma}{2} a^2\left(1 - \frac{y^2}{b^2}\right)\mathrm{d}y.
$$
于是从 $-b$ 到 $b$ 积分便得到椭圆形薄板所受的压力
$$
\begin{aligned}
P &= \int_{-b}^{b} \frac{\gamma}{2} a^{2} \left(1 - \frac{y^{2}}{b^{2}}\right) dy \\
&= \gamma a^{2} \int_{0}^{b} \left(1 - \frac{y^{2}}{b^{2}}\right) dy \\
&= \gamma a^{2} \left(b - \frac{y^{3}}{3b^{2}} \Big|_{0}^{b}\right) \\
&= \frac{2\gamma}{3} a^{2} b.
\end{aligned}
$$
**评注** 在定积分的分割、近似、求和、取极限这四步法中关键是分割与近似,抓住了这个关键,我们把这个方法简化为微元分析法。作适当分割取微元是为了近似,找到函数改变量的主要部分,从而直接写出所求函数的微分表达式,再积分便得到所求的量。
在【例3.30】的【解法一】中,作横向分割,任取 $[x, x + \Delta x]$ 对应的小横条薄板,把变压强转化为常压强,从而得到压力函数改变量的近似值 $\Delta P \approx \gamma x \cdot 2y\Delta x$,$\Delta x \to 0$ 时近似式转化为等式 $\frac{\mathrm{d}P}{\mathrm{d}x} = 2\gamma xy$,即
$$
\mathrm{d}P = 2\gamma x y \mathrm{d}x.
$$
在【解法二】中,作纵向分割,任取 $[y, y + \Delta y]$ 对应的小竖条薄板,虽然压强是变量,但小竖条的长度转化为常量,即可近似看成矩形,对矩形薄板(如图3.19),它所受的压力为
$$
\begin{aligned}
P &= \int_{a}^{b} \gamma x c dx = \frac{1}{2} \gamma c (b^{2} - a^{2}) \\
&= \gamma \cdot \frac{b + a}{2} (b - a) c \\
&= \text{矩形中心处的压强} \times \text{矩形面积}.
\end{aligned}
$$
因此也是可行的。
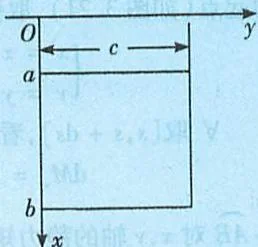
图3.19
## (二)变力做功
1. 设一物体沿 $x$ 轴运动,在运动过程中始终有力 $F$ 作用于物体上。力 $F$ 的方向或与 $Ox$ 轴方向一致(此时 $F$ 取正值)或与 $Ox$ 轴方向相反(此时 $F$ 取负值)。物体在 $x$ 处的力为 $F(x)$,则物体从 $a$ 移到 $b$ 时变力 $F(x)$ 做的功为
$$
W = \int_{a}^{b} F(x) \mathrm{d}x \quad (\text{任取 } [x, x + \mathrm{d}x] \text{ 一段,力 } F(x) \text{ 做的功 } \mathrm{d}W = F(x) \mathrm{d}x).
$$
2. 设有一容器(如图3.20),其顶部所在平面与 $Ox$ 轴(铅直向下)相交于原点,液体表面与 $Ox$ 轴相截于 $x = a$,底面与 $Ox$ 轴相截于 $x = b$,垂直于 $Ox$ 轴的平面截容器所得的截面面积为 $x$ 的连续函数 $S(x)$,则将容器中的液体全部抽出所做的功为
$$
W = \int_{a}^{b}\rho gxS(x)\mathrm{d}x,
$$
其中 $\rho$ 为液体密度,$g$ 为重力加速度。(有关例子参见【例3.59】)
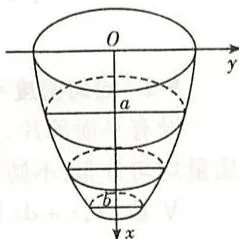
图3.20
## (三)引力问题
质量分别为 $m_{1}, m_{2}$ 相距为 $r$ 的两质点间的引力的大小为 $F = k \frac{m_{1} m_{2}}{r^{2}}$,其中 $k$ 为引力常数,引力的方向沿着两质点的连线方向。(有关例子参见本章题型训练四、6题)
## (四)质心或形心问题
这类问题的核心是静力矩的计算原理。设平面上有 $n$ 个质点:
$$
A_{1}(x_{1}, y_{1}), A_{2}(x_{2}, y_{2}), \dots, A_{n}(x_{n}, y_{n}),
$$
质量分别为 $m_{1}, m_{2}, \dots, m_{n}$,这 $n$ 个质点对 $x, y$ 轴的静力矩为 $my_{i}$, $mx_{i} (i = 1, 2, \dots, n)$;
而质点组对 $x, y$ 轴的静力矩分别为 $M_{x} = \sum_{i=1}^{n} m_{i}y_{i}$, $M_{y} = \sum_{i=1}^{n} m_{i}x_{i}$;
质量为 $M = \sum_{i=1}^{n} m_i$,设质点组的质心 $(\overline{x}, \overline{y})$,则 $\overline{x} = \frac{M_y}{M}$,$\overline{y} = \frac{M_z}{M}$。
### 1. 均匀线密度为 $\rho$ 的平面曲线的质心(形心)
考虑质量均匀分布的平面光滑物体曲线 $\widehat{AB}$,其线密度为常数 $\rho$,$\widehat{AB}$ 的全长为 $l$,以 $A$ 点为计算弧长的起点(如图3.21),取弧长 $s$ 为自变量,$0 \leqslant s \leqslant l$,则 $\widehat{AB}$ 的参数方程(以弧长 $s$ 为参数)为
$$
\left\{
\begin{array}{l}
x = x(s), \\
y = y(s)
\end{array}
\right. \quad (0 \leqslant s \leqslant l).
$$
$\forall$ 取 $[s, s + \mathrm{d}s]$,看作质点,坐标为 $(x(s), y(s))$,小微元的质量为 $\rho \mathrm{d}s \Rightarrow$ 静力矩微元
$$
\mathrm{d}M_{x} = y(s) \rho \mathrm{d}s, \quad \mathrm{d}M_{y} = x(s) \rho \mathrm{d}s,
$$
$\Rightarrow \widehat{AB}$ 对 $x, y$ 轴的静力矩分别为 $M_x = \int_0^l y(s)\rho \mathrm{d}s$, $M_y = \int_0^l x(s)\rho \mathrm{d}s$,
$\widehat{AB}$ 的质量 $M = \int_{0}^{l}\rho \mathrm{d}s = \rho l$,设 $\widehat{AB}$ 的质心(形心)为 $(\overline{x},\overline{y})$,则
$$
\overline{x} = \frac{M_y}{M} = \frac{1}{l} \int_{0}^{l} x(s) ds, \quad \overline{y} = \frac{M_x}{M} = \frac{1}{l} \int_{0}^{l} y(s) ds.
$$
若 $\widehat{AB}$ 的参数方程是
$$
\left\{
\begin{array}{l}
x = \varphi(t), \\
y = \psi(t)
\end{array}
\right. \quad (\alpha \leqslant t \leqslant \beta),
$$
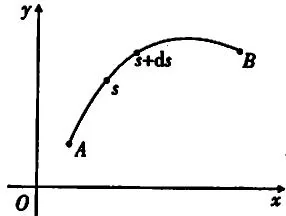
图3.21
其中 $\varphi(t),\psi(t)$ 在 $[\alpha ,\beta ]$ 有连续的导数,由变量替换及弧微分公式得 $\widehat{AB}$ 的质心(形心) $(\overline{x},\overline{y})$ 为
$$
\bar{x} = \frac{\int_{\alpha}^{\beta} \varphi(t) \sqrt{\varphi^{\prime 2}(t) + \psi^{\prime 2}(t)} dt}{\int_{\alpha}^{\beta} \sqrt{\varphi^{\prime 2}(t) + \psi^{\prime 2}(t)} dt}, \quad \bar{y} = \frac{\int_{\alpha}^{\beta} \psi(t) \sqrt{\varphi^{\prime 2}(t) + \psi^{\prime 2}(t)} dt}{\int_{\alpha}^{\beta} \sqrt{\varphi^{\prime 2}(t) + \psi^{\prime 2}(t)} dt}.
$$
### 2. 均匀密度平面图形的质心(形心)
设有平面薄片,所占的平面图形是 $D: a \leqslant x \leqslant b, g(x) \leqslant y \leqslant f(x)$,其中 $f(x), g(x)$ 在 $[a, b]$ 连续,质量均匀分布,不妨设面密度为1。求它的质心 $(\overline{x}, \overline{y})$。见图3.22。
$\forall$ 取 $[x, x + \mathrm{d}x]$ 与之相应的小窄条,其质量为 $[f(x) - g(x)] \mathrm{d}x$,质心为 $\left(x, \frac{1}{2} [f(x) + g(x)]\right)$,静力矩为
$$
\mathrm{d}M_{y} = x [f(x) - g(x)] \mathrm{d}x,
$$
$$
\begin{aligned}
\mathrm{d}M_{x} &= \frac{1}{2} [f(x) + g(x)] [f(x) - g(x)] \mathrm{d}x \\
&= \frac{1}{2} [f^{2}(x) - g^{2}(x)] dx.
\end{aligned}
$$
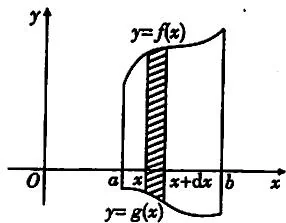
图3.22
整个图形的静力矩为 $M_y = \int_a^b x[f(x) - g(x)]\mathrm{d}x$,$M_{x} = \frac{1}{2}\int_{a}^{b}[f^{2}(x) - g^{2}(x)]\mathrm{d}x$。
总质量 $M = \int_{a}^{b}[f(x) - g(x)]\mathrm{d}x$,因此,质心 $(\overline{x},\overline{y})$ 为
$$
\bar{x} = \frac{M_{y}}{M} = \frac{\int_{a}^{b} x [f(x) - g(x)] \mathrm{d}x}{\int_{a}^{b} [f(x) - g(x)] \mathrm{d}x}, \quad \bar{y} = \frac{M_{x}}{M} = \frac{\frac{1}{2} \int_{a}^{b} [f^{2}(x) - g^{2}(x)] \mathrm{d}x}{\int_{a}^{b} [f(x) - g(x)] \mathrm{d}x}.
$$
该均匀平面薄片的质心也叫作这平面薄片所占的平面图形 $D$ 的形心。因此,求质心与求形心有相同的公式。有关例子参见题型十四之3。
## (五)函数在区间上的平均值
设函数 $y = f(x)$ 在区间 $[a,b]$ 上连续,则 $f(x)$ 在 $[a,b]$ 上的平均值为 $\bar{y} = \frac{1}{b - a}\int_{a}^{b}f(x)\mathrm{d}x$。

# 考题型及其解题方法与技巧
## 题型一 有关原函数与定积分概念的命题
【例3.31】设 $f(x)$ 是连续函数,并满足 $\int f(x)\sin x\mathrm{d}x = \cos^2 x + C$,又 $F(x)$ 是 $f(x)$ 的原函数,且满足 $F(0) = 0$,则 $F(x) =$ ________。
【分析】由题设及原函数存在定理可知,$F(x) = \int_0^x f(t)\mathrm{d}t$。为求 $f(x)$,将题设等式求导得
$$
f(x) \sin x = \left[ \int f(x) \sin x dx \right]^{\prime} = (\cos^{2} x + C)^{\prime} = -2 \sin x \cos x,
$$
从而 $f(x) = -2\cos x$,于是
$$
F(x) = \int_{0}^{x} f(t) dt = \int_{0}^{x} -2 \cos t dt = -2 \sin x.
$$
【例3.32】设 $f(x)$ 为连续函数,且满足 $f(x) = x + \int_0^1 xf(x)\mathrm{d}x$,则 $f(x) = \underline{\quad}$
【分析】定积分是积分和的极限,当被积函数和积分区间确定后,它就是一个确定的数。从而由题设知可令 $\int_{0}^{1} x f(x) \mathrm{d}x = A$,只要求得常数 $A$ 就可得到函数 $f(x)$ 的表达式。为此将题设等式两边同乘 $x$ 并从0到1求定积分,就有
$$
A = \int_{0}^{1} x^{2} \mathrm{d}x + \int_{0}^{1} A x \mathrm{d}x \Leftrightarrow A = \frac{1}{3} + \frac{1}{2} A \Leftrightarrow A = \frac{2}{3}.
$$
故 $f(x) = x + \frac{2}{3}$。
## 题型二 积分值的比较或积分值符号的判断
【例3.33】设 $M = \int_{0}^{\frac{\pi}{2}}\sin (\sin x)\mathrm{d}x$,$N = \int_0^{\frac{\pi}{2}}\cos (\cos x)\mathrm{d}x$,则有
(A) $M < 1 < N$
(B) $M < N < 1$
(C) $N < M < 1$
(D) $1 < M < N$
【分析】 $\sin (\sin x),\cos (\cos x)$ 均在 $\left[0,\frac{\pi}{2}\right]$ 上连续,由 $\sin x\leqslant x\Rightarrow \sin (\sin x) \leqslant \sin x\left(x\in \left[0,\frac{\pi}{2}\right]\right)$,
$\int_{0}^{\frac{\pi}{2}} \sin (\sin x) \, \mathrm{d}x < \int_{0}^{\frac{\pi}{2}} \sin x \, \mathrm{d}x = 1$,即 $M < 1$。
又 $\int_{0}^{\frac{\pi}{2}}\cos (\cos x)\mathrm{d}x \xrightarrow{x = \frac{\pi}{2} - t} \int_{0}^{\frac{\pi}{2}}\cos (\sin t)\mathrm{d}t >
---
# 练习题
根据文档内容,我生成以下涵盖核心概念、定理和方法的例题:
### 例题1
**题目内容**
设一矩形薄板垂直立于水中,其宽度为2米,高度为4米,且上边与水面齐平。已知水的比重为γ,求水对薄板的侧压力。
**题目解答**
建立坐标系:取水面为x轴,垂直向下为x轴正方向,薄板位于x∈[0,4]。在深度x处取微元条,宽度为2,高度为dx,面积为2dx。
压强为γx,故微元压力dP = γx·2dx = 2γx dx
总压力P = ∫₀⁴ 2γx dx = 2γ [x²/2]₀⁴ = 2γ × 8 = 16γ
因此水对薄板的侧压力为16γ。
---
### 例题2
**题目内容**
设物体沿x轴运动,受力F(x) = 3x² + 2x(单位:N),求物体从x=1移动到x=3时变力所做的功。
**题目解答**
变力做功公式:W = ∫ₐᵇ F(x)dx
W = ∫₁³ (3x² + 2x)dx = [x³ + x²]₁³
= (27 + 9) - (1 + 1) = 36 - 2 = 34 J
故变力做功为34焦耳。
---
### 例题3
**题目内容**
求均匀密度平面曲线y = x²(0 ≤ x ≤ 1)的形心坐标。
**题目解答**
曲线弧长微分ds = √(1 + (dy/dx)²)dx = √(1 + 4x²)dx
总弧长L = ∫₀¹ √(1 + 4x²)dx
形心坐标:
x̄ = (1/L)∫₀¹ x√(1 + 4x²)dx
ȳ = (1/L)∫₀¹ x²√(1 + 4x²)dx
计算得:L = (1/4)[2x√(1+4x²) + ln|2x+√(1+4x²)|]₀¹ = (1/4)(2√5 + ln(2+√5))
x̄ = (1/L)·(1/12)((1+4x²)³/²)₀¹ = (1/L)·(1/12)(5√5 - 1)
ȳ = (1/L)·(1/64)[8x(1+4x²)³/² - 2x√(1+4x²) - ln|2x+√(1+4x²)|]₀¹
代入计算可得具体数值解。
---
### 例题4
**题目内容**
计算反常积分∫₁^∞ dx/(x√(x²+1))的敛散性。
**题目解答**
当x→+∞时,1/(x√(x²+1)) ~ 1/x²
由于∫₁^∞ dx/x²收敛,由比较判别法知原积分收敛。
计算积分值:令x = tanθ,dx = sec²θdθ
∫ dx/(x√(x²+1)) = ∫ sec²θdθ/(tanθsecθ) = ∫ cscθdθ
= ln|cscθ - cotθ| + C = ln|(√(x²+1)-1)/x| + C
因此∫₁^∞ dx/(x√(x²+1)) = lim[b→∞] ln|(√(b²+1)-1)/b| - ln|(√2-1)/1|
= 0 - ln(√2-1) = ln(1/(√2-1)) = ln(√2+1)
---
### 例题5
**题目内容**
设f(x)在[0,1]连续,且∫₀¹ f(x)dx = 0,∫₀¹ xf(x)dx = 1。证明存在ξ∈(0,1)使得f(ξ) > 4。
**题目解答**
反证法:假设对所有x∈[0,1]有f(x) ≤ 4
则∫₀¹ xf(x)dx ≤ 4∫₀¹ xdx = 4 × 1/2 = 2
但已知∫₀¹ xf(x)dx = 1,不产生矛盾。
考虑函数g(x) = 4x - 2,满足∫₀¹ g(x)dx = 0,∫₀¹ xg(x)dx = 1
若f(x) ≤ 4x - 2,则∫₀¹ xf(x)dx ≤ ∫₀¹ x(4x-2)dx = 4/3 - 1 = 1/3 < 1
矛盾!因此存在ξ∈(0,1)使f(ξ) > 4ξ - 2 ≥ -2
但需要更强结论。实际上,假设f(x) ≤ 4,则∫₀¹ xf(x)dx ≤ 4∫₀¹ xdx = 2,不能推出矛盾。
正确证法:假设f(x) ≤ 4,考虑h(x) = f(x) - 4x + 2
∫₀¹ h(x)dx = ∫₀¹ f(x)dx - 4∫₀¹ xdx + 2 = 0 - 2 + 2 = 0
∫₀¹ xh(x)dx = ∫₀¹ xf(x)dx - 4∫₀¹ x²dx + 2∫₀¹ xdx = 1 - 4/3 + 1 = 2/3 > 0
由积分中值定理,存在ξ使h(ξ) > 0,即f(ξ) > 4ξ - 2
当ξ∈(0,1)时,4ξ - 2 ∈ (-2,2),不能保证f(ξ) > 4。
实际上,取f(x) = 6x - 2满足条件,且f(1) = 4,在x接近1时f(x)接近4。
因此原命题需要调整,典型反例表明结论不一定成立。Last updated on