八、方向导数与梯度
(一)方向导数
1. 方向导数的概念
平面上过点 \(M_0(x_0, y_0)\) 以 \(l = (\cos \alpha, \cos \beta)\) 为方向向量的直线 \(L\) 的参数方程:
\[x = x _ {0} + t \cos \alpha , y = y _ {0} + t \cos \beta .\]\(z = f(x,y)\) 限制在直线 \(L\) 上(见图8.2)变化时就变成了一元函数
\[\varphi (t) = f \left(x _ {0} + t \cos \alpha , y _ {0} + t \cos \beta\right).\]【定义8.8】 若存在极限
\[\varphi^ {\prime} (0) = \lim _ {t \rightarrow 0} \frac {f \left(x _ {0} + t \cos \alpha , y _ {0} + t \cos \beta\right) - f \left(x _ {0} , y _ {0}\right)}{t},\]称它为 \(z = f(x,y)\) 在点 \(M_0(x_0,y_0)\) 沿方向 \(\iota\) 的方向导数,记为 \(\frac{\partial f(x_0,y_0)}{\partial l}\) 或 \(\left.\frac{\partial f}{\partial l}\right|_{(x_0,y_0)}\)。
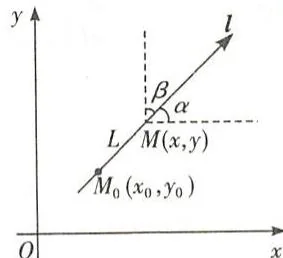
图8.2
2. 方向导数的存在性与计算公式
【定理8.14】 设 \(z = f(x,y)\) 在 \(M_0(x_0,y_0)\) 处可微,则 \(f(x,y)\) 在 \(M_0\) 点沿任意方向 \(\boldsymbol {l} = (\cos \alpha ,\cos \beta)\) 存在方向导数且
\[\frac{\partial f(x_0,y_0)}{\partial l} = \frac{\partial f(x_0,y_0)}{\partial x}\mathrm{cos}\alpha +\frac{\partial f(x_0,y_0)}{\partial y}\mathrm{cos}\beta .\]在平面上 \(l\) 除了用方向角表示外也可用极角表示:\(l = (\cos \theta ,\sin \theta)\),\(\theta\) 是 \(l\) 的极角,\(\theta \in [0,2\pi)\),此时相应的方向导数的计算公式是
\[\frac{\partial f(x_0,y_0)}{\partial l} = \frac{\partial f(x_0,y_0)}{\partial x}\cos \theta +\frac{\partial f(x_0,y_0)}{\partial y}\sin \theta .\]【定理8.15】 设三元函数 \(u = f(x,y,z)\) 在 \(M_0(x_0,y_0,z_0)\) 处可微,则 \(f(x,y,z)\) 在 \(M_0\) 点沿任意方向 \(\pmb{l} = (\cos \alpha ,\cos \beta ,\cos \gamma)\) 存在方向导数且有
\[\frac {\partial f \left(x _ {0} , y _ {0} , z _ {0}\right)}{\partial l} = \frac {\partial f \left(x _ {0} , y _ {0} , z _ {0}\right)}{\partial x} \cos \alpha + \frac {\partial f \left(x _ {0} , y _ {0} , z _ {0}\right)}{\partial y} \cos \beta + \frac {\partial f \left(x _ {0} , y _ {0} , z _ {0}\right)}{\partial z} \cos \gamma .\](二)梯度(向量)与方向导数的最大值
函数 \(z = f(x,y)\) 在点 \(M_0\) 的方向导数计算公式可改写成
\[\begin{aligned} \frac {\partial f \left(x _ {0} , y _ {0}\right)}{\partial l} &= \left(\frac {\partial f \left(x _ {0} , y _ {0}\right)}{\partial x}, \frac {\partial f \left(x _ {0} , y _ {0}\right)}{\partial y}\right) \cdot (\cos \alpha , \cos \beta) \\ &= \operatorname {grad} f \left(x _ {0}, y _ {0}\right) \cdot l = | \operatorname {grad} f \left(x _ {0}, y _ {0}\right) | \cos \langle \operatorname {grad} f \left(x _ {0}, y _ {0}\right), l \rangle , \end{aligned}\]这里向量 \(\mathbf{grad}f(x_0,y_0) = \left(\frac{\partial f(x_0,y_0)}{\partial x},\frac{\partial f(x_0,y_0)}{\partial y}\right)\) 称为 \(z = f(x,y)\) 在点 \(M_0\) 的梯度(向量)。
\(\frac{\partial f(x_0,y_0)}{\partial l}\) 随 \(l\) 而变化,当 \(l = \frac{\operatorname{grad}f(x_0,y_0)}{|\operatorname{grad}f(x_0,y_0)|}\) 即沿梯度方向时,方向导数取最大值 \(|\operatorname {grad}f(x_0,y_0)|\)。由此可见,函数在某点的梯度是这样一个向量,它的方向是函数在该点的方向导数最大的方向,它的模是最大方向导数的值。
【例8.13】 求函数 \(u = \ln (x + \sqrt{y^2 + z^2})\) 在点 \(A(1,0,1)\) 沿点 \(A\) 指向 \(B(3, - 2,2)\) 方向的方向导数。
【解】 先求AB的方向余弦:\(\overrightarrow{AB} = (3 - 1, - 2 - 0,2 - 1) = (2, - 2,1)\)
\[l = \overrightarrow {A B} / | \overrightarrow {A B} | = (\cos \alpha , \cos \beta , \cos \gamma) = \frac {1}{3} (2, - 2, 1).\]再求 \(\left.\mathbf{grad}u\right|_{(1,0,1)} = \left(\frac{\partial u}{\partial x},\frac{\partial u}{\partial y},\frac{\partial u}{\partial z}\right)\bigg|_{(1,0,1)}\)
\[= \left. \frac {1}{x + \sqrt {y ^ {2} + z ^ {2}}} \left(1, \frac {y}{\sqrt {y ^ {2} + z ^ {2}}}, \frac {z}{\sqrt {y ^ {2} + z ^ {2}}}\right) \right| _ {(1, 0, 1)} = \left(\frac {1}{2}, 0, \frac {1}{2}\right).\]于是 \(\left.\frac{\partial u}{\partial l}\right|_{(1,0,1)} = \left.\frac{\partial u}{\partial x}\right|_{(1,0,1)}\cos \alpha +\left.\frac{\partial u}{\partial y}\right|_{(1,0,1)}\cos \beta +\left.\frac{\partial u}{\partial z}\right|_{(1,0,1)}\cos \gamma\)
\[= \frac {1}{2} \times \frac {2}{3} + \frac {1}{2} \times \frac {1}{3} = \frac {1}{2}.\]练习题
例题1
计算函数 \(f(x, y) = x^2 + 3xy\) 在点 \((1, 2)\) 沿方向 \(\mathbf{l} = (\cos \frac{\pi}{3}, \sin \frac{\pi}{3})\) 的方向导数。
解答
首先计算函数在点 \((1, 2)\) 的偏导数:
在点 \((1, 2)\) 处:
\[\frac{\partial f}{\partial x}(1, 2) = 2(1) + 3(2) = 8, \quad \frac{\partial f}{\partial y}(1, 2) = 3(1) = 3.\]方向 \(\mathbf{l} = (\cos \frac{\pi}{3}, \sin \frac{\pi}{3}) = \left( \frac{1}{2}, \frac{\sqrt{3}}{2} \right)\)。
根据方向导数公式:
因此,方向导数为 \(4 + \frac{3\sqrt{3}}{2}\)。
例题2
设函数 \(g(x, y, z) = xyz + e^{x+y}\),求其在点 \((0, 1, 2)\) 沿方向 \(\mathbf{l} = \left( \frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}} \right)\) 的方向导数。
解答
计算函数在点 \((0, 1, 2)\) 的偏导数:
在点 \((0, 1, 2)\) 处:
\[\frac{\partial g}{\partial x}(0, 1, 2) = (1)(2) + e^{0+1} = 2 + e, \quad \frac{\partial g}{\partial y}(0, 1, 2) = (0)(2) + e^{0+1} = e, \quad \frac{\partial g}{\partial z}(0, 1, 2) = (0)(1) = 0.\]方向 \(\mathbf{l} = \left( \frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}} \right)\)。
根据方向导数公式:
因此,方向导数为 \(\frac{2 + 2e}{\sqrt{3}}\)。
例题3
求函数 \(h(x, y) = x^2 - y^2\) 在点 \((2, 1)\) 的梯度向量,并确定使方向导数最大的方向及其最大值。
解答
计算函数在点 \((2, 1)\) 的偏导数:
在点 \((2, 1)\) 处:
\[\frac{\partial h}{\partial x}(2, 1) = 4, \quad \frac{\partial h}{\partial y}(2, 1) = -2.\]梯度向量为:
\[\mathbf{grad} \, h(2, 1) = (4, -2).\]梯度的模为:
\[|\mathbf{grad} \, h(2, 1)| = \sqrt{4^2 + (-2)^2} = \sqrt{16 + 4} = \sqrt{20} = 2\sqrt{5}.\]使方向导数最大的方向是梯度方向:
\[\mathbf{l}_{\text{max}} = \frac{\mathbf{grad} \, h(2, 1)}{|\mathbf{grad} \, h(2, 1)|} = \frac{(4, -2)}{2\sqrt{5}} = \left( \frac{2}{\sqrt{5}}, -\frac{1}{\sqrt{5}} \right).\]最大方向导数为梯度的模:
\[\left. \frac{\partial h}{\partial l} \right|_{\text{max}} = |\mathbf{grad} \, h(2, 1)| = 2\sqrt{5}.\]因此,最大方向导数为 \(2\sqrt{5}\),方向为 \(\left( \frac{2}{\sqrt{5}}, -\frac{1}{\sqrt{5}} \right)\)。