六、积分学应用的基本方法——微元分析法
定积分所计算的是某函数改变量,如曲边梯形的面积是面积函数改变量,弧长是弧长函数改变量。所用方法是分割、近似、求和、取极限这四步法,即
\[F(b) - F(a) \xlongequal{\text{整体改变量化为}} \sum_{i=1}^{n} \left[ F(x_{i}) - F(x_{i-1}) \right] \xlongequal[\text{近似函数改变量}]{\text{局部上用微分}} \sum_{i=1}^{n} F^{\prime}(x_{i}) \Delta x_{i} = \sum_{i=1}^{n} f(x_{i}) \Delta x_{i}.\]取极限从近似转化为精确,即
\[F(b) - F(a) = \lim_{\lambda \rightarrow 0} \sum_{i=1}^{n} f\left(x_{i}\right) \Delta x_{i} = \int_{a}^{b} f(x) dx.\]这四步法中的关键是分割与近似,从微分式与积分式的等价性来看:若 \(f(x)\) 在 \([a,b]\) 上连续,则
\[\mathrm{d}F(x) = f(x) \mathrm{d}x (\forall x \in [a,b]) \Leftrightarrow \int_{a}^{x} f(t) \mathrm{d}t = F(x) - F(a) (\forall x \in [a,b]).\]这四步法归结为两步:
第一步,求出 \(F(x)\) 的微分式 \(\mathrm{d}F(x) = f(x)\mathrm{d}x\),其中 \(f(x)\) 是已知的,\(F(x)\) 是要求的;
第二步,将微分式积分,即 \(F(b) - F(a) = \int_{a}^{b}f(x)\mathrm{d}x\)
怎样写出 \(F(x)\) 的微分式,常用的方法是微元分析法:任取微元区间 \([x, x + \Delta x]\),求出 \(\Delta F(x) = F(x + \Delta x) - F(x) \approx f(x) \Delta x\)。当 \(\Delta x \to 0\) 时上面的近似式转化为等式,即 \(\mathrm{d}F(x) = f(x) \mathrm{d}x\)。
例3.24
求一块铅直平板如图3.1所示在某种液体(比重为 \(\gamma\))中所受的压力
解
液体中深度为 \(h\) 处所受的压强为 \(p = h\gamma\),从深度为 \(a\) 到 \(x\) 之间平板所受的压力记为 \(P(x)\),任取 \([x, x + \Delta x]\) 上小横条,所受压力为
\[\Delta P = P(x + \Delta x) - P(x) \approx x \gamma \cdot c \Delta x.\]令 \(\Delta x\to 0\),得 \(\mathrm{d}P(x) = x\gamma c\mathrm{d}x\)。于是,总压力为
\[\begin{aligned} P &= \int_{a}^{b} x \gamma c dx = \frac{\gamma c}{2} (b^{2} - a^{2}) \\ &= \gamma \cdot \frac{1}{2} (a + b) c (b - a) = \gamma \cdot \text{矩形中心的深度} \cdot \text{矩形的面积}. \end{aligned}\]注
近似公式 \(\Delta F \approx f(x) \Delta x\) 转化为等式 \(\mathrm{d}F(x) = f(x) \mathrm{d}x\) 的关键是:\(\Delta F\) 与 \(f(x) \Delta x\) 的误差是 \(\Delta x\) 的高阶无穷小(\(\Delta x \to 0\) 时)。
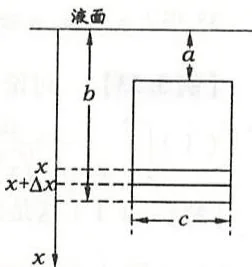
图3.1
练习题
例题1
用微元分析法推导半径为 \(R\) 的圆的面积公式。
解答
将圆看作由无数个同心圆环组成。取半径 \(r \in [0, R]\),微元区间 \([r, r + \Delta r]\) 对应的圆环面积近似为
当 \(\Delta r \to 0\) 时,有 \(\mathrm{d}A = 2\pi r \mathrm{d}r\)。积分得
\[A = \int_0^R 2\pi r \mathrm{d}r = \pi R^2.\]例题2
设一物体沿直线运动,速度 \(v(t) = 3t^2 + 2t\)(米/秒)。用微元分析法求在时间区间 \([1, 4]\) 内物体的位移。
解答
位移函数为 \(s(t)\),微元区间 \([t, t + \Delta t]\) 上的位移增量
当 \(\Delta t \to 0\) 时,\(\mathrm{d}s = (3t^2 + 2t)\mathrm{d}t\)。积分得
\[s = \int_1^4 (3t^2 + 2t) \mathrm{d}t = \left[ t^3 + t^2 \right]_1^4 = (64 + 16) - (1 + 1) = 78 \text{米}.\]例题3
一铅直平板浸入水中,形状为高 \(H\)、底边宽 \(L\) 的等腰三角形,顶点位于水面。设水的比重为 \(\gamma\),用微元分析法求平板所受水压力。
解答
建立坐标系:以水面为 \(y = 0\),向下为 \(y\) 轴正方向。在深度 \(y\) 处,平板宽度为 \(l(y) = \frac{L}{H} y\)。取微元区间 \([y, y + \Delta y]\),压力增量
当 \(\Delta y \to 0\) 时,\(\mathrm{d}P = \frac{\gamma L}{H} y^2 \mathrm{d}y\)。积分得
\[P = \int_0^H \frac{\gamma L}{H} y^2 \mathrm{d}y = \frac{\gamma L}{H} \cdot \frac{H^3}{3} = \frac{\gamma L H^2}{3}.\]例题4
验证函数 \(F(x) = \ln x\) 在区间 \([1, e]\) 上满足微分关系 \(\mathrm{d}F(x) = \frac{1}{x} \mathrm{d}x\),并计算 \(\int_1^e \frac{1}{x} \mathrm{d}x\).
解答
由 \(F(x) = \ln x\) 得 \(F'(x) = \frac{1}{x}\),故 \(\mathrm{d}F(x) = \frac{1}{x} \mathrm{d}x\)。
积分得
结果与直接积分一致。