八、一元函数微分学的简单应用

（一）平面曲线的切线与法线

1. 用显式方程表示的平面曲线

若平面曲线 $C$ 的方程为 $y = f(x)(a \leqslant x \leqslant b)$，则曲线 $C$ 在点 $M_0(x_0, y_0) (y_0 = f(x_0))$ 处的切线方程为 $y = y_0 + f'(x_0)(x - x_0)$，其中 $f(x)$ 在点 $x_0$ 处可导，在点 $M_0$ 处的法线方程为

\[y = y _ {0} - \frac {1}{f ^ {\prime} (x _ {0})} (x - x _ {0}) \quad (f ^ {\prime} (x _ {0}) \neq 0), \quad x = x _ {0} \quad (f ^ {\prime} (x _ {0}) = 0), (\text {见图} 2. 4).\]

当 $\lim_{x\to x_0}\frac{f(x) - f(x_0)}{x - x_0} = \infty$ 且 $f(x)$ 在点 $x_0$ 处连续时，则 $C$ 在 $M_0$ 点的切线方程为 $x = x_0$（见图2.5）。

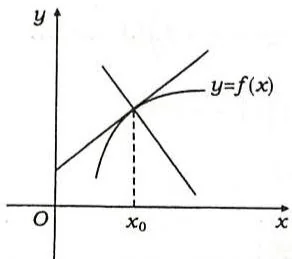
图2.4

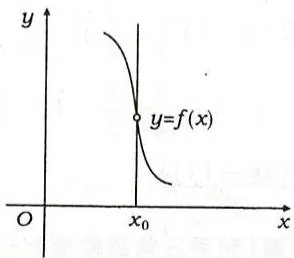
图2.5

2. 用参数方程表示的平面曲线

若平面曲线 $C$ 的参数方程为 $x = x(t), y = y(t) (\alpha \leqslant t \leqslant \beta)$，则曲线 $C$ 在点 $M_0(x_0, y_0) ((x_0, y_0) = (x(t_0), y(t_0))$）处的切线方程与法线方程分别为

\[\frac {x - x _ {0}}{x ^ {\prime} \left(t _ {0}\right)} = \frac {y - y _ {0}}{y ^ {\prime} \left(t _ {0}\right)}, \quad \frac {x - x _ {0}}{- y ^ {\prime} \left(t _ {0}\right)} = \frac {y - y _ {0}}{x ^ {\prime} \left(t _ {0}\right)},\]

其中，$(x^{\prime}(t_0),y^{\prime}(t_0))$ 为曲线 $C$ 在点 $M_0$ 的切向量，$x(t),y(t)$ 在 $t_0$ 可导且 $x^{\prime 2}(t_0) + y^{\prime 2}(t_0)\neq 0$。

3. 用极坐标方程表示的平面曲线

若平面曲线 $C$ 的极坐标方程为 $r = r(\theta)$（$\alpha \leqslant \theta \leqslant \beta$），则曲线 $C$ 的参数方程为

\[x = r (\theta) \cos \theta , y = r (\theta) \sin \theta \quad (\alpha \leqslant \theta \leqslant \beta).\]

由此可得曲线的切线的斜率，其中 $r(\theta)$ 可导。

4. 用隐式方程表示的平面曲线

若平面曲线 $C$ 的隐式方程为 $f(x,y) = 0$，其中 $f(x,y)$ 有连续的一阶偏导数，则曲线 $C$ 在点 $M_0(x_0, y_0)$ 处的切线方程为

\[\frac {\partial f \left(x _ {0} , y _ {0}\right)}{\partial x} \left(x - x _ {0}\right) + \frac {\partial f \left(x _ {0} , y _ {0}\right)}{\partial y} \left(y - y _ {0}\right) = 0,\]

这里 $\left(\frac{\partial f(x_0,y_0)}{\partial x},\frac{\partial f(x_0,y_0)}{\partial y}\right)$ 是切线的法向量，也是曲线 $C$ 在点 $M_0$ 的法向量。

【例2.19】设曲线 $y = x^{2} + ax + b$ 和 $2y = -1 + xy^3$ 在点(1，-1）处相切，其中 $a,b$ 是常数，则

(A) $a = 0, b = 2$

(B) $a = 1, b = -3$

(D) $a = -1, b = -1$

【分析】曲线 $y = x^{2} + ax + b$ 在点（1，-1）处的斜率

\[y ^ {\prime} = \left(x ^ {2} + a x + b\right) ^ {\prime} \mid_ {x = 1} = 2 + a.\]

将方程 $2y = -1 + xy^3$ 对 $x$ 求导得 $2y' = y^3 + 3xy^2y'$。由此知，该曲线在 $(1, -1)$ 处的斜率 $y'(1)$ 为 $2y'(1) = (-1)^3 + 3y'(1)$，$y'(1) = 1$。因这两条曲线在 $(1, -1)$ 处相切，所以在该点它们的斜率相同，即 $2 + a = 1, a = -1$。又曲线 $y = x^2 + ax + b$ 过点 $(1, -1)$，所以 $1 + a + b = -1, b = -2 - a = -1$。因此选(D)。

【例2.20】对数螺线 $r = \mathrm{e}^{\theta}$ 在点 $(r,\theta) = \left(\mathrm{e}^{\dagger},\frac{\pi}{2}\right)$ 处的切线的直角坐标方程为

【分析】对数螺线的参数方程为 $\left\{ \begin{array}{l} x = r \cos \theta = e^{\theta} \cos \theta, \\ y = r \sin \theta = e^{\theta} \sin \theta, \end{array} \right.$ 于是它在点 $\left(e^{\frac{\pi}{2}}, \frac{\pi}{2}\right)$ 处切线的斜率为

\[\frac {\mathrm {d} y}{\mathrm {d} x} = \left. \frac {y ^ {\prime} (\theta)}{x ^ {\prime} (\theta)} \right| _ {\theta = \frac {1}{2}} = \left. \frac {\mathrm {e} ^ {\theta} (\sin \theta + \cos \theta)}{\mathrm {e} ^ {\theta} (\cos \theta - \sin \theta)} \right| _ {\theta = \frac {1}{2}} = - 1.\]

当 $\theta = \frac{\pi}{2}$ 时 $x = 0, y = e^{\pm}$。因此该切线方程为 $y = e^{\pm} - x$。

（二）平面曲线的曲率

平面曲线的曲率与曲率圆等问题是一元函数微分学与积分学的综合应用，我们在第三章（一元函数积分概念、计算及应用）来讲述该内容（见第三章七（三））。

（三）用导数描述某些物理量

设有变量 $x$ 与 $y$ 之间的函数关系 $y = f(x)$。$f'(x_0)$ 表示 $y = f(x)$ 在 $x = x_0$ 处随 $x$ 的变化率。

实际中除了速度是路程函数的导数之外，常用的还有：

(1) 一根杆从一端0点算起，$[0, x]$ 段杆的质量为 $m = m(x)$，则杆在点 $x$ 处的线密度

\[\rho (x) = m ^ {\prime} (x).\]

（2）一根导线在 $[0, t]$ 这段时间内通过导线横截面的电量为 $Q = Q(t)$，则导线在 $t$ 时刻的电流强度

\[I (t) = Q ^ {\prime} (t).\]

(3) 某单位质量的物体从某确定的温度升高到温度 $T$ 时所需的热量为 $q(T)$，则物体在温度 $T$ 时的比热 $C(T) = q'(T)$。

(4) 某力在 $[0, t]$ 时间内所做的功 $w = w(t)$，则 $t$ 时刻的功率为 $w'(t)$。

题型一有关一元函数的导数与微分概念的命题

【例2.21】设 $f(x_0) \neq 0, f(x)$ 在 $x = x_0$ 连续，则 $f(x)$ 在 $x_0$ 可导是 $|f(x)|$ 在 $x_0$ 可导的（）条件

(A) 充分非必要

（B）充分必要

（D）既非充分也非必要

【分析】由 $f(x_0) \neq 0 \Rightarrow f(x_0) > 0$ 或 $f(x_0) < 0$，因 $f(x)$ 在点 $x_0$ 处连续，则 $f(x)$ 在 $x_0$ 某邻域是保号的，即 $\exists \delta > 0$，当 $|x - x_0| < \delta$ 时，

\[f (x) \left\{ \begin{array}{l l} {> 0 ,} & {f (x _ {0}) > 0 \text {时} ,} \\ {< 0 ,} & {f (x _ {0}) < 0 \text {时}} \end{array} \right. \Rightarrow | x - x _ {0} | < \delta \text {时} , f (x) = \left\{ \begin{array}{l l} {| f (x) |,} & {f (x _ {0}) > 0 ,} \\ {- | f (x) |,} & {f (x _ {0}) < 0 ,} \end{array} \right.\]

因此应选(B)。

【例2.22】设 $f(x)$ 在点 $x = x_0$ 处可导，且 $f(x_0) = 0$，则 $f'(x_0) = 0$ 是 $|f(x)|$ 在 $x_0$ 可导的（）条件。

(A) 充分非必要

（B）充分必要

（C）必要非充分

（D）既非充分也非必要

【分析】按定义 $|f(x)|$ 在 $x_0$ 可导 $\Leftrightarrow \lim_{x\to x_0}\frac{|f(x)| - |f(x_0)|}{x - x_0} = \lim_{x\to x_0}\frac{|f(x)|}{x - x_0}$ 存在，

即 $\lim_{x\to x_0 + }\frac{|f(x)|}{x - x_0} (\geqslant 0),\lim_{x\to x_0 - }\frac{|f(x)|}{x - x_0} (\leqslant 0)$ 均存在且相等

\[\Leftrightarrow \lim _ {x \rightarrow x _ {0}} \frac {| f (x) |}{x - x _ {0}} = 0 \Leftrightarrow \lim _ {x \rightarrow x _ {0}} \frac {| f (x) - f \left(x _ {0}\right) |}{| x - x _ {0} |} = 0 \Leftrightarrow \lim _ {x \rightarrow x _ {0}} \frac {f (x) - f \left(x _ {0}\right)}{x - x _ {0}} = f ^ {\prime} \left(x _ {0}\right) = 0.\]

因此应选（B）。

评注 ① 这里用到了：$\lim_{x\to x_0}g(x) = 0\iff \lim_{x\to x_0}|g(x)| = 0$

②【例 2.21】与【例 2.22】给出了 $\left| {f\left( x\right) }\right|$ 与 $f\left( x\right)$ 可导性之间的关系。

题型二两一元函数乘积的可导性的讨论

【例2.23】设 $F(x) = g(x)\varphi (x),\varphi (x)$ 在 $x = a$ 连续但不可导，又 $g^{\prime}(a)$ 存在，则 $g(a) = 0$ 是 $F(x)$ 在 $x = a$ 可导的（）条件。

(A) 充分必要

（B）充分非必要

（D）既非充分也非必要

【分析】① 因为 $\varphi'(a)$ 不存在，所以不能对 $g(x)\varphi(x)$ 用乘积的求导法则；② 当 $g(a) \neq 0$ 时，若 $F(x)$ 在 $x = a$ 可导，可对 $\frac{F(x)}{g(x)}$ 用商的求导法则。

（I）若 $g(a) = 0$，按定义考察

\[\frac {F (x) - F (a)}{x - a} = \frac {g (x) \varphi (x) - g (a) \varphi (a)}{x - a} = \frac {g (x) - g (a)}{x - a} \varphi (x),\]

则 $\lim_{x\to a}\frac{F(x) - F(a)}{x - a} = \lim_{x\to a}\frac{g(x) - g(a)}{x - a}\lim_{x\to a}\varphi (x) = g'(a)\varphi (a),$

即 $F^{\prime}(a) = g^{\prime}(a)\varphi (a)$。

（Ⅱ）再用反证法证明：若 $F^{\prime}(a)$ 存在，则必有 $g(a) = 0$ 若 $g(a)\neq 0$，由商的求导法则即知 $\varphi (x)$

$= \frac{F(x)}{g(x)}$ 在 $x = a$ 可导，与假设条件 $\varphi(a)$ 在 $x = a$ 处不可导矛盾。因此应选(A)。

评注设 $g(x)$ 在 $x = a$ 可导，$\varphi(x)$ 在 $x = a$ 连续而不可导，则

\[g (x) \varphi (x) \text {在} x = a \text {处} \left\{ \begin{array}{l l} \text {不可导，} & \text {若} g (a) \neq 0, \\ \text {可导且导数为} g ^ {\prime} (a) \varphi (a), & \text {若} g (a) = 0. \end{array} \right.\]

【例2.24】函数 $f(x) = (x^{2} - x - 2) \mid x^{3} - x \mid$ 的不可导点有

(A) 3个。

(B) 2个。

(D) 0个。

【分析】函数 $|x|, |x - 1|, |x + 1|$ 分别仅在 $x = 0, x = 1, x = -1$ 不可导且它们处处连续。因此只需在这些点考察 $f(x)$ 是否可导，为此或用【例2.23】的结论，或按定义考察。

方法 $1^{\circ}$ 用【例2.23】的结论来判断。$f(x) = (x^{2} - x - 2)|x||x - 1||x + 1|$，只需考察 $x = 0,1,-1$ 是否可导。

考察 $x = 0$，令 $g(x) = (x^{2} - x - 2)\mid x^{2} - 1\mid$，则 $f(x) = g(x)\mid x\mid ,g^{\prime}(0)$ 存在，$g(0)\neq 0$，$\varphi (x)$ $= |x|$ 在 $x = 0$ 连续但不可导，故 $f(x)$ 在 $x = 0$ 不可导。

考察 $x = 1$，令 $g(x) = (x^{2} - x - 2)|x^{2} + x|$，$\varphi (x) = |x - 1|$，则 $g^{\prime}(1)$ 存在，$g(1)\neq 0,\varphi (x)$ 在 $x = 1$ 连续但不可导，故 $f(x) = g(x)\varphi (x)$ 在 $x = 1$ 不可导。

考察 $x = -1$，令 $g(x) = (x^{2} - x - 2)|x^{2} - x|$，$\varphi (x) = |x + 1|$，则 $g^{\prime}(-1)$ 存在，$g(-1) = 0$，$\varphi (x)$ 在 $x = -1$ 连续但不可导，故 $f(x) = g(x)\varphi (x)$ 在 $x = -1$ 可导。因此选(B)。

方法 $2^{\circ}$ 按定义考察。

在 $x = 0$ 处 $\frac{f(x) - f(0)}{x} = (x^2 - x - 2)|x^2 - 1|\frac{|x|}{x}$，于是

\[f _ {+} ^ {\prime} (0) = \lim _ {x \rightarrow 0 +} \frac {f (x) - f (0)}{x} --- # 练习题 ### 例题1 求曲线 $ y = x^3 - 3x + 2 $ 在点 $ (1, 0) $ 处的切线方程和法线方程。 **解答** 首先求导数： $ y' = 3x^2 - 3 $。在点 $ x = 1 $ 处，斜率 $ k = y'(1) = 3(1)^2 - 3 = 0 $。切线方程为： $ y - 0 = 0 \cdot (x - 1) \Rightarrow y = 0 $。由于切线斜率为 0，法线垂直于切线，法线方程为： $ x = 1 $。 --- ### 例题2 设曲线由参数方程 $ x = t^2, y = t^3 $ 给出，求在点 $ (1, 1) $ 处的切线方程。 **解答** 对应参数 $ t = 1 $。求导： $ \frac{dx}{dt} = 2t, \quad \frac{dy}{dt} = 3t^2 $。在 $ t = 1 $ 处： $ \frac{dy}{dx} = \frac{3(1)^2}{2(1)} = \frac{3}{2} $。切线方程为： $ y - 1 = \frac{3}{2}(x - 1) \Rightarrow y = \frac{3}{2}x - \frac{1}{2} $。 --- ### 例题3 设曲线由极坐标方程 $ r = 2\cos\theta $ 给出，求在 $ \theta = \frac{\pi}{3} $ 处的切线斜率。 **解答** 参数化： $ x = r\cos\theta = 2\cos^2\theta, \quad y = r\sin\theta = 2\cos\theta\sin\theta $。求导： $ \frac{dx}{d\theta} = -4\cos\theta\sin\theta, \quad \frac{dy}{d\theta} = 2(\cos^2\theta - \sin^2\theta) $。在 $ \theta = \frac{\pi}{3} $ 处： $ \frac{dy}{dx} = \frac{2(\cos^2\frac{\pi}{3} - \sin^2\frac{\pi}{3})}{-4\cos\frac{\pi}{3}\sin\frac{\pi}{3}} = \frac{2(\frac{1}{4} - \frac{3}{4})}{-4 \cdot \frac{1}{2} \cdot \frac{\sqrt{3}}{2}} = \frac{-1}{-\sqrt{3}} = \frac{1}{\sqrt{3}} $。切线斜率为 $ \frac{1}{\sqrt{3}} $。 --- ### 例题4 设曲线由隐式方程 $ x^2 + y^2 - 2xy = 1 $ 给出，求在点 $ (1, 1) $ 处的切线方程。 **解答** 令 $ F(x, y) = x^2 + y^2 - 2xy - 1 $。求偏导： $ F_x = 2x - 2y, \quad F_y = 2y - 2x $。在点 $ (1, 1) $ 处： $ F_x = 0, \quad F_y = 0 $。由于两个偏导均为 0，需用极限定义求切线。考虑 $ y = 1 + k(x - 1) $ 代入方程，解得 $ k = 1 $。切线方程为： $ y - 1 = 1 \cdot (x - 1) \Rightarrow y = x $。 --- ### 例题5 设 $ f(x) = |x^2 - 1| $，讨论 $ f(x) $ 在 $ x = 1 $ 处的可导性。 **解答** 在 $ x = 1 $ 附近：若 $ x > 1 $，则 $ f(x) = x^2 - 1 $，$ f'(x) = 2x $，右导数 $ f'_+(1) = 2 $。若 $ x < 1 $，则 $ f(x) = 1 - x^2 $，$ f'(x) = -2x $，左导数 $ f'_-(1) = -2 $。由于 $ f'_+(1) \ne f'_-(1) $，函数在 $ x = 1 $ 处不可导。 --- ### 例题6 设 $ f(x) = (x - 1)|x - 2| $，求 $ f(x) $ 的不可导点。 **解答** 函数在 $ x = 2 $ 处可能不可导。令 $ g(x) = x - 1, \varphi(x) = |x - 2| $。在 $ x = 2 $ 处： $ g(2) = 1 \ne 0 $，且 $ \varphi(x) $ 在 $ x = 2 $ 连续但不可导，因此 $ f(x) = g(x)\varphi(x) $ 在 $ x = 2 $ 不可导。其他点均可导，故不可导点为 $ x = 2 $。 --- ### 例题7 设 $ f(x) = \begin{cases} x^2 \sin\frac{1}{x}, & x \ne 0 \\ 0, & x = 0 \end{cases} $，求 $ f'(0) $。 **解答** 按定义： $ f'(0) = \lim_{x \to 0} \frac{f(x) - f(0)}{x - 0} = \lim_{x \to 0} \frac{x^2 \sin\frac{1}{x}}{x} = \lim_{x \to 0} x \sin\frac{1}{x} = 0 $。所以 $ f'(0) = 0 $。 --- ### 例题8 设 $ y = \ln(1 + x^2) $，求 $ \frac{dy}{dx} $ 和 $ \frac{d^2y}{dx^2} $。 **解答** $ \frac{dy}{dx} = \frac{2x}{1 + x^2} $。 $ \frac{d^2y}{dx^2} = \frac{2(1 + x^2) - 2x \cdot 2x}{(1 + x^2)^2} = \frac{2 - 2x^2}{(1 + x^2)^2} $。 --- ### 例题9 设 $ y = \int_0^x e^{t^2} dt $，求反函数 $ x = \varphi(y) $ 的二阶导数 $ \frac{d^2x}{dy^2} $。 **解答** 由 $ \frac{dy}{dx} = e^{x^2} $，得 $ \frac{dx}{dy} = e^{-x^2} $。 $ \frac{d^2x}{dy^2} = \frac{d}{dx}(e^{-x^2}) \cdot \frac{dx}{dy} = -2x e^{-x^2} \cdot e^{-x^2} = -2x e^{-2x^2} $。 --- ### 例题10 设曲线 $ y = x^2 + ax + b $ 与直线 $ y = 2x + 1 $ 在点 $ (1, 3) $ 处相切，求 $ a, b $。 **解答** 曲线在 $ (1, 3) $ 处斜率： $ y' = 2x + a $，在 $ x = 1 $ 处为 $ 2 + a $。切线与直线 $ y = 2x + 1 $ 斜率相同： $ 2 + a = 2 \Rightarrow a = 0 $。曲线过点 $ (1, 3) $： $ 3 = 1 + 0 + b \Rightarrow b = 2 $。所以 $ a = 0, b = 2 $。\]

八、一元函数微分学的简单应用

（一）平面曲线的切线与法线

1. 用显式方程表示的平面曲线

2. 用参数方程表示的平面曲线

3. 用极坐标方程表示的平面曲线

4. 用隐式方程表示的平面曲线

（二）平面曲线的曲率

（三）用导数描述某些物理量

题型一 有关一元函数的导数与微分概念的命题

题型二 两一元函数乘积的可导性的讨论

题型一有关一元函数的导数与微分概念的命题

题型二两一元函数乘积的可导性的讨论