五、多元函数积分学的几何应用
(一)空间图形的体积
- 平行截面面积为已知的立体的体积(见第三章七(四)1.)
- 旋转体的体积(见第三章七(四)2.)
- 柱形长条区域的体积
(1)设 \(z = z_{1}(x,y)\),\(z = z_{2}(x,y)\) 在有界闭区域 \(D\) 上连续,\(z_{1}(x,y)\leqslant z_{2}(x,y)\)。\(\Omega\) 是由曲面 \(z = z_{1}(x,y),z = z_{2}(x,y)\) 及以 \(D\) 的边界为准线,母线平行于 \(z\) 轴的柱面所围成的空间区域(可称为柱形长条区域,如图9.34),则 \(\varOmega\) 的体积为
\[V = \iiint_{\Omega} \mathrm{d}V = \iint_{D} \left(\int_{z_{1}(x,y)}^{z_{2}(x,y)} \mathrm{d}z\right) \mathrm{d}x\mathrm{d}y = \iint_{D} \left[ z_{2}(x,y) - z_{1}(x,y) \right] \mathrm{d}x\mathrm{d}y.\](2)特别地,\(z_{1}(x,y) = 0,z_{2}(x,y) = f(x,y)\),得曲顶柱体的体积为
\[V = \iint_{D} f(x,y) \mathrm{d}x\mathrm{d}y.\]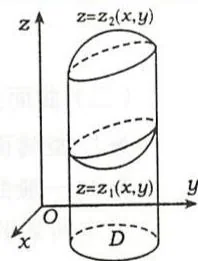
图9.34
【例9.30】设 \(\Omega\) 为曲面 \(x^{2} + y^{2} = az\) 与 \(z = 2a - \sqrt{x^2 + y^2}\) 所围成的空间区域(如图9.35),求它的体积,其中 \(a > 0\)
【解法一】用柱形长条区域的体积公式——求一个二重积分。
由 \(\left\{ \begin{array}{l} x^2 + y^2 = az, \\ z = 2a - \sqrt{x^2 + y^2} \end{array} \right.\) 消去 \(z\),得投影柱面 \(x^2 + y^2 = a^2\),于是,\(\Omega\) 在 \(xy\) 平面上投影区域 \(D: x^2 + y^2 \leq a^2\)。该立体
\[\Omega = \left\{(x, y, z) \mid \frac{x^{2} + y^{2}}{a} \leqslant z \leqslant 2a - \sqrt{x^{2} + y^{2}}, (x, y) \in D \right\},\]因此,\(\Omega\) 的体积为
\[\begin{aligned} V &= \iint_{D} \left(2a - \sqrt{x^{2} + y^{2}} - \frac{x^{2} + y^{2}}{a}\right) dxdy = \int_{0}^{2\pi} d\theta \int_{0}^{a} \left(2a - r - \frac{r^{2}}{a}\right) rdr \\ &= 2\pi \left(ar^{2} - \frac{1}{3}r^{3} - \frac{r^{4}}{4a}\right) \Bigg|_{0}^{a} = \frac{5}{6}\pi a^{3}. \end{aligned}\]【解法二】用三重积分表示区域 \(\Omega\) 的体积公式。区域 \(\Omega\) 的体积为 \(V = \iiint_{\Omega} \mathrm{d}x\,\mathrm{d}y\,\mathrm{d}z\)。
用先二后一的顺序求这个三重积分。如【解法一】,求得曲面 \(x^{2} + y^{2} = az\) 与 \(z = 2a - \sqrt{x^2 + y^2}\) 的交线是 \(\left\{ \begin{array}{l} x^2 + y^2 = a^2, \\ z = a. \end{array} \right.\) 过 \(z\) 轴上点 \(z\) 与 \(z\) 轴垂直的平面截 \(\Omega\) 得平面区域 \(D(z)\),则 \(D(z)\) 的面积为
\[S(z) = \left\{ \begin{array}{ll} \pi az, & 0 \leqslant z \leqslant a, \\ (2a - z)^{2}\pi, & a \leqslant z \leqslant 2a. \end{array} \right.\]因此,\(\Omega\) 的体积为
\[\begin{aligned} V &= \int_{0}^{2a} \left(\iint_{D(z)} \mathrm{d}x\mathrm{d}y\right) \mathrm{d}z = \int_{0}^{a} \pi az\mathrm{d}z + \int_{a}^{2a} \pi(2a - z)^{2}\mathrm{d}z \\ &= \frac{1}{2}\pi az^{2} \Big|_{0}^{a} + \frac{1}{3}\pi(z - 2a)^{3} \Big|_{a}^{2a} = \frac{\pi}{2}a^{3} + \frac{\pi}{3}a^{3} = \frac{5}{6}\pi a^{3}. \end{aligned}\]【解法三】直接用定积分求旋转体的体积。求 \(\Omega\) 的体积,即求由 \(yz\) 平面上的曲线
\[y = \sqrt{az} (0 \leqslant z \leqslant a), y = 2a - z (a \leqslant z \leqslant 2a).\]绕 \(z\) 轴旋转而成的旋转体的体积,按旋转体体积公式得
\[V = \pi \int_{0}^{2a} y^{2}(z)\mathrm{d}z = \pi \int_{0}^{a} az\mathrm{d}z + \pi \int_{a}^{2a} (2a - z)^{2}\mathrm{d}z = \frac{5}{6}\pi a^{3}.\](二)曲面面积
- 旋转面的面积(见第三章七之(五))
- 一般曲面的面积
设空间某平面图形的面积为 \(A\),该平面图形在 \(xy\) 平面上的投影的面积为 \(\sigma\),则
\[A = \frac{\sigma}{|\cos\gamma|},\]其中 \(\gamma\) 是平面的法向量 \(n\) 与 \(z\) 轴正向的夹角(图9.36)
(1)设曲面 \(S\) 由方程 \(z = f(x,y) ((x,y)\in D)\) 给出,\(D\) 为 \(S\) 在 \(xy\) 平面上的投影区域,\(f(x,y)\) 在有界闭区域 \(D\) 有连续的偏导数 \(f_{x}^{\prime},f_{y}^{\prime},S\) 上任意点处的单位法向量 \(\pmb{n} = (\cos\alpha,\cos\beta,\cos\gamma) = \pm \frac{1}{\sqrt{1 + f_x'^2 + f_y'^2}} (-f_x', - f_y',1)\),则 \(S\) 的面积为
\[A = \iint_{D} \frac{\mathrm{d}\sigma}{|\cos\gamma|} = \iint_{D} \sqrt{1 + f_{x}^{\prime 2} + f_{y}^{\prime 2}} \mathrm{d}x\mathrm{d}y,\]其中 \(\gamma\) 是曲面 \(S\) 的法向量与 \(z\) 轴正向的夹角。
(2)若曲面 \(S\) 的方程为 \(x = g(y, z) ((y, z) \in D_{yz})\) 或 \(y = h(z, x) ((z, x) \in D_{zx})\),则可得类似的曲面面积计算公式。
(3)柱面被曲面所截部分的面积:设有 \(Oxy\) 平面上的光滑曲线 \(L\),以 \(L\) 为准线,母线平行于 \(z\) 轴作柱面,此柱面在 \(xy\) 平面与连续曲面 \(z = f(x, y) (\geqslant 0)\) 之间部分的面积为 \(A = \int_{L} f(x, y) \mathrm{d}s\)。

图9.35
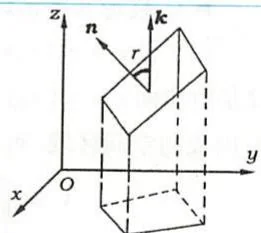
图9.36
【例9.31】求柱面 \(x^{2} + y^{2} = ax\) 含于球面 \(x^{2} + y^{2} + z^{2} = a^{2}\) 内的曲面面积 \(S\),其中 \(a > 0\) 为常数。
【分析与解法一】由对称性只需考虑第一卦限部分。将柱面方程表成 \(y\) 为 \(x\) 的函数是方便的:\(y = \sqrt{ax - x^2}\)。于是 \(S = 4\iint_{D} \sqrt{1 + y'_x^2 + y'_z^2} \,\mathrm{d}z\,\mathrm{d}x\),\(D\) 是这部分柱面在 \(Ozx\) 平面的投影区域,求出 \(D\) 的关键是求柱面与球面的交线在 \(Ozx\) 平面的投影曲线。见图9.37。
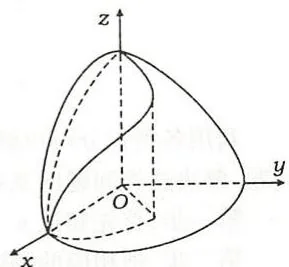
图9.37
柱面与球面的交线为 \(\left\{ \begin{array}{l} x^2 + y^2 + z^2 = a^2, \\ x^2 + y^2 = ax, \end{array} \right.\) 它在 \(Ozx\) 平面上的投影曲线为抛物线 \(z^2 = a^2 - ax\),它与 \(Ox\) 轴,\(Oz\) 轴围成区域 \(D\),则所求曲面面积为
\[\begin{aligned} S &= 4 \iint_{D} \sqrt{1 + y^{\prime 2}_{x} + y^{\prime 2}_{z}} \mathrm{d}z\mathrm{d}x = 4 \iint_{D} \sqrt{1 + \left(\frac{a - 2x}{2y}\right)^{2}} \mathrm{d}z\mathrm{d}x = 4 \iint_{D} \frac{a\mathrm{d}z\mathrm{d}x}{2\sqrt{ax - x^{2}}} \\ &= 4 \int_{0}^{a} \mathrm{d}x \int_{0}^{\sqrt{a^{2} - ax}} \frac{a}{2\sqrt{ax - x^{2}}} \mathrm{d}z = 2a \int_{0}^{a} \frac{\sqrt{a^{2} - ax}}{\sqrt{ax - x^{2}}} \mathrm{d}x = 2a \int_{0}^{a} \sqrt{a} \sqrt{\frac{(a - x)x}{ax - x^{2}}} \sqrt{\frac{1}{x}} \mathrm{d}x \\ &= 2a \sqrt{a} \int_{0}^{a} \sqrt{\frac{1}{x}} \mathrm{d}x = 4a \sqrt{a} \sqrt{x} \Bigg|_{0}^{a} = 4a^{2}. \end{aligned}\]【分析与解法二】同样,由对称性只需考虑第一卦限部分。利用柱面被曲面所截部分的面积公式得
\[S = 4 \int_{L} \sqrt{a^{2} - x^{2} - y^{2}} ds,\]其中 \(L: x^2 + y^2 = ax (0 \leqslant x \leqslant a, y \geqslant 0)\),即 \(y = \sqrt{ax - x^2} (0 \leqslant x \leqslant a)\)。因为
\[\sqrt{1 + y^{\prime 2}} = \sqrt{1 + \left(\frac{a - 2x}{2\sqrt{ax - x^{2}}}\right)^{2}} = \frac{a}{2\sqrt{ax - x^{2}}}\]所以 \(S = 4\int_{0}^{a}\sqrt{a^2 - ax}\sqrt{1 + y'^2}\mathrm{d}x = 2\int_{0}^{a}\frac{a^{3/2}}{\sqrt{x}}\mathrm{d}x = 4a^2\)。

评注
① 设有 \(Oxy\) 平面上的光滑曲线 \(L\),以 \(L\) 为准线,母线平行于 \(z\) 轴作柱面,此柱面在 \(xy\) 平面与连续曲面 \(z = f(x, y) (\geqslant 0)\) 之间部分的面积为
\[S = \int_{L} f(x, y) ds.\]本题中【分析与求解二】用的就是这个公式。
② 我们也可用圆周 \(L:x^{2} + y^{2} = ax(0\leqslant x\leqslant a,y\geqslant 0)\),即 \(\left(x - \frac{a}{2}\right)^2 +y^2 = \left(\frac{a}{2}\right)^2\) 的参数方程 \(x = \frac{a}{2} +\frac{a}{2}\cos t,y = \frac{a}{2}\sin t(0\leqslant t\leqslant \pi)\) 来计算 \(S\)。由于 \(\mathrm{ds} = \sqrt{x'^2(t) + y'^2(t)}\mathrm{dt} = \frac{a}{2}\mathrm{dt},a^2 -x^2 -y^{2} = a^{2} - ax = \frac{a^{2}}{2} (1 - \cos t)\),于是
\[\begin{aligned} S &= 4 \int_{L} \sqrt{a^{2} - x^{2} - y^{2}} ds = 4 \int_{0}^{\pi} \frac{a}{\sqrt{2}} \sqrt{1 - \cos t} \cdot \frac{a}{2} dt \\ &= 2a^{2} \int_{0}^{\pi} \sin \frac{t}{2} \mathrm{d}t = 4a^{2} \int_{0}^{\frac{\pi}{2}} \sin u \mathrm{d}u = 4a^{2} (-\cos u) \Bigg|_{0}^{\frac{\pi}{2}} = 4a^{2}. \end{aligned}\]③ 【分析与求解一】中对曲面 \(y = y(z,x),(z,x)\in D\),用的是面积计算公式
\[S = \iint_{D} \sqrt{1 + y_{x}^{\prime 2} + y_{z}^{\prime 2}} dxdz,\]其中关键的步骤是对具体的曲面,求它在 \(zx\) 坐标面上的投影区域 \(D\)。
练习题
例题1
求由曲面 \(z = x^2 + y^2\) 与 \(z = 4 - x^2 - y^2\) 所围成的空间区域 \(\Omega\) 的体积。
【题目解答】 两曲面的交线由方程组
\[\begin{cases} z = x^2 + y^2, \\ z = 4 - x^2 - y^2 \end{cases}\]消去 \(z\) 得 \(x^2 + y^2 = 2\),因此投影区域 \(D: x^2 + y^2 \leq 2\)。
在 \(D\) 上,\(x^2 + y^2 \leq 4 - x^2 - y^2\),故
体积为
\[V = \iint_D \left[ (4 - x^2 - y^2) - (x^2 + y^2) \right] \, dx \, dy = \iint_D (4 - 2x^2 - 2y^2) \, dx \, dy.\]利用极坐标:\(x = r\cos\theta, y = r\sin\theta\),则
\[V = \int_0^{2\pi} d\theta \int_0^{\sqrt{2}} (4 - 2r^2) r \, dr = 2\pi \left[ 2r^2 - \frac{1}{2}r^4 \right]_0^{\sqrt{2}} = 2\pi (4 - 2) = 4\pi.\]例题2
求曲面 \(z = \sqrt{x^2 + y^2}\) 被柱面 \(x^2 + y^2 = 2x\) 所截部分的面积。
【题目解答】 曲面方程为 \(z = f(x,y) = \sqrt{x^2 + y^2}\),偏导数为
\[f_x = \frac{x}{\sqrt{x^2 + y^2}}, \quad f_y = \frac{y}{\sqrt{x^2 + y^2}}.\]面积元素为
\[dA = \sqrt{1 + f_x^2 + f_y^2} \, dx \, dy = \sqrt{1 + \frac{x^2 + y^2}{x^2 + y^2}} \, dx \, dy = \sqrt{2} \, dx \, dy.\]柱面 \(x^2 + y^2 = 2x\) 即 \((x-1)^2 + y^2 = 1\),投影区域 \(D\) 为该圆盘。
由对称性,只需计算第一象限部分并乘以 4:
其中 \(D_1\) 为第一象限部分面积 \(\frac{\pi}{4}\)。
因此总面积为
例题3
设区域 \(\Omega\) 由曲面 \(z = \sqrt{x^2 + y^2}\) 与 \(z = 1\) 围成,求 \(\Omega\) 的体积。
【题目解答】 投影区域 \(D: x^2 + y^2 \leq 1\),在 \(D\) 上 \(\sqrt{x^2 + y^2} \leq 1\),故
\[\Omega = \left\{ (x,y,z) \mid \sqrt{x^2 + y^2} \leq z \leq 1, (x,y) \in D \right\}.\]体积为
\[V = \iint_D \left[ 1 - \sqrt{x^2 + y^2} \right] dx \, dy.\]用极坐标:
\[V = \int_0^{2\pi} d\theta \int_0^1 (1 - r) r \, dr = 2\pi \left[ \frac{r^2}{2} - \frac{r^3}{3} \right]_0^1 = 2\pi \left( \frac{1}{2} - \frac{1}{3} \right) = \frac{\pi}{3}.\]例题4
求曲面 \(z = xy\) 在区域 \(D: x^2 + y^2 \leq 1\) 上的面积。
【题目解答】 曲面 \(z = f(x,y) = xy\),偏导数为
\[f_x = y, \quad f_y = x.\]面积元素为
\[dA = \sqrt{1 + f_x^2 + f_y^2} \, dx \, dy = \sqrt{1 + x^2 + y^2} \, dx \, dy.\]面积为
\[A = \iint_D \sqrt{1 + x^2 + y^2} \, dx \, dy.\]用极坐标:
\[A = \int_0^{2\pi} d\theta \int_0^1 \sqrt{1 + r^2} \cdot r \, dr = 2\pi \cdot \frac{1}{2} \int_0^1 \sqrt{1 + u} \, du \quad (u = r^2).\]计算得
\[A = \pi \cdot \frac{2}{3} (1 + u)^{3/2} \Big|_0^1 = \frac{2\pi}{3} (2\sqrt{2} - 1).\]