六、多元函数的极值问题

（一）多元函数极值及驻点的概念

【定义 8.6】 若 $\exists M_0(x_0,y_0)$ 的某邻域 $U(M_0,\delta)$，使得

\[f(x, y) \leqslant f\left(x_{0}, y_{0}\right) \quad \left(f(x, y) \geqslant f\left(x_{0}, y_{0}\right)\right), \forall (x, y) \in U\left(M_{0}, \delta\right),\]

则称 $f(x,y)$ 在点 $M_0$ 有极大值（极小值）$f(x_0,y_0)$。极大值与极小值统称为极值。点 $M_0$ 为 $f(x,y)$ 的极大值点（极小值点），统称为极值点。

【定义 8.7】 凡是能使 $f_{x}^{\prime}(x,y) = 0, f_{y}^{\prime}(x,y) = 0$ 同时成立的点 $(x,y)$ 称为 $z = f(x,y)$ 的驻点。

（二）多元函数取得极值的必要条件与充分条件

1. 多元函数取得极值的必要条件（以二元函数为例）

【定理 8.12】 设 $f(x,y)$ 在点 $(x_0,y_0)$ 处具有偏导数，且在点 $(x_0,y_0)$ 处取极值，则它在该点的偏导数必然为零，即 $f_{x}^{\prime}(x_{0},y_{0}) = 0$，$f_{y}^{\prime}(x_{0},y_{0}) = 0$。

【注】 具有偏导数的极值点必然是驻点，但驻点不一定是极值点。

2. 多元函数取得极值的充分条件

【定理 8.13】 设 $z = f(x,y)$ 在点 $(x_0,y_0)$ 的某邻域内连续且有一阶及二阶连续偏导 $f_{x}^{\prime}(x_{0},y_{0}) = 0,f_{y}^{\prime}(x_{0},y_{0}) = 0$，令 $f_{xx}^{\prime \prime}(x_0,y_0) = A,f_{xy}^{\prime \prime}(x_0,y_0) = B,f_{yy}^{\prime \prime}(x_0,y_0) = C,$ 则

(1) $AC - B^2 > 0$ 时，$f(x, y)$ 在 $(x_0, y_0)$ 取极值，且当 $A > 0$ 时取极小值，$A < 0$ 时取极大值；
(2) $AC - B^2 < 0$ 时，$(x_0,y_0)$ 不是 $f(x,y)$ 的极值点；
(3) $AC - B^2 = 0$ 时，$f(x, y)$ 在 $(x_0, y_0)$ 可能取极值，也可能不取极值，还需另作讨论（一般用极值定义）。

3. 求二元函数极值点的一般步骤

若 $z = f(x,y)$ 有连续的二阶偏导数，则可按如下方法求它的极值点：

第一步，解方程组 $f_{x}^{\prime}(x,y) = 0, f_{y}^{\prime}(x,y) = 0$ 求得所有驻点；

第二步，对每个驻点求出二阶偏导数的值

\[A = f_{x x}^{\prime \prime}\left(x_{0}, y_{0}\right), \quad B = f_{x y}^{\prime \prime}\left(x_{0}, y_{0}\right), \quad C = f_{y y}^{\prime \prime}\left(x_{0}, y_{0}\right);\]

第三步，定出 $AC - B^2$ 的符号，按【定理 8.13】的结论判定 $f(x_0,y_0)$ 是否取极值，是极大值还是极小值。

【例 8.10】 设 $z(x,y) = x^3 +y^3 -3xy$

(I) $-\infty < x < +\infty, -\infty < y < +\infty$，求 $z(x,y)$ 的驻点与极值点。
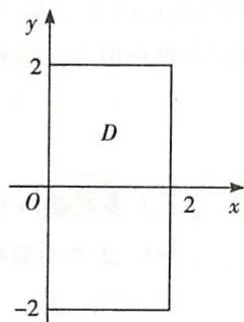
(II) $D = \{(x, y) \mid 0 \leqslant x \leqslant 2, -2 \leqslant y \leqslant 2\}$，求证：$D$ 内的唯一极值点不是 $z(x, y)$ 在 $D$ 上的最值点。

【分析与求解】（I）解方程组

\[\left\{ \begin{array}{l} \frac {\partial z}{\partial x} = 3 x ^ {2} - 3 y = 0 \\ \frac {\partial z}{\partial y} = 3 y ^ {2} - 3 x = 0 \end{array} \right.\]

得全部驻点 $(0,0)$ 与 $(1,1)$。再求

\[\frac {\partial^ {2} z}{\partial x ^ {2}} = 6 x, \frac {\partial^ {2} z}{\partial x \partial y} = - 3, \frac {\partial^ {2} z}{\partial y ^ {2}} = 6 y\]

考察

\[\left( \begin{array}{ll}A & B\\ B & C \end{array} \right) = \left( \begin{array}{ll}\frac{\partial^2z}{\partial x^2} & \frac{\partial^2z}{\partial x\partial y}\\ \frac{\partial^2z}{\partial x\partial y} & \frac{\partial^2z}{\partial y^2} \end{array} \right) = \left( \begin{array}{ll}6x & -3\\ -3 & 6y \end{array} \right)\]

$(0,0)$ 处 $\left( \begin{array}{ll}A & B\\ B & C \end{array} \right) = \left( \begin{array}{ll}0 & -3\\ -3 & 0 \end{array} \right),AC - B^2 < 0\Rightarrow (0,0)$ 不是极值点
$(1,1)$ 处 $\left( \begin{array}{cc}A & B\\ B & C \end{array} \right) = \left( \begin{array}{cc}6 & -3\\ -3 & 6 \end{array} \right),AC - B^2 >0,A > 0\Rightarrow (1,1)$ 是极小值点。

因此 $z(x,y)$ 的驻点是 $(0,0),(1,1)$，极值点是 $(1,1)$ 且是极小值点。

（Ⅱ）$D$ 内唯一极值点 $(1,1)$ 是极小值点，$z(1,1) = -1$

$D$ 的边界点 $(0, -2)$ 处

\[z(0, - 2) = (- 2) ^ {3} = - 8 < z(1, 1)\]

因 $z(x,y)$ 在有界闭区域 $D$ 上连续，必存在最小值，

又 $z(0, -2) < z(1, 1), (0, -2) \in D \Rightarrow z(1, 1)$ 不是 $z(x, y)$ 在 $D$ 的最小值。

$图示$

评注该例说明了多元函数与一元函数的一个区别。设连续的一元函数 $y = f(x)$ 在区间 I 有唯一的极值点，若是极小（大）值点，则就是 $f(x)$ 在区间 I 上的最小（大）值点。对于多元函数没有相应的结论，即区域 $D$ 上连续的二元函数 $f(x, y)$ 在 $D$ 有唯一的极值点，若是极小（大）值点，不一定是 $f(x, y)$ 在 $D$ 的最小（大）值点。

（三）条件极值点的必要条件

设 $f(x,y),\varphi (x,y)$ 在点 $P_{0}(x_{0},y_{0})$ 的某邻域有连续的一阶偏导数且 $\varphi_y^\prime (x_0,y_0)\neq 0.$ 若 $P_{0}(x_{0},y_{0})$ 是二元函数 $z = f(x,y)$ 在条件 $\varphi (x,y) = 0$ 下的极值点，则

\[\left\{ \begin{array}{l} \left| \begin{array}{cc}f_{x}^{\prime}(P_{0}) & f_{y}^{\prime}(P_{0})\\ \varphi_{x}^{\prime}(P_{0}) & \varphi_{y}^{\prime}(P_{0}) \end{array} \right| = 0,\\ \varphi (P_{0}) = 0 \end{array} \right. \tag{8.9}\]

等价于

\[\left\{ \begin{array}{l}f_{x}^{\prime}(P_{0}) + \lambda \varphi_{x}^{\prime}(P_{0}) = 0,\\ f_{y}^{\prime}(P_{0}) + \lambda \varphi_{y}^{\prime}(P_{0}) = 0,\\ \varphi (P_{0}) = 0. \end{array} \right.\]

【注】 该命题的证明参见本章题型训练三、20题。

练习题

例题1

求函数 $f(x, y) = x^2 + y^2 - 4x - 6y + 13$ 的驻点，并判断这些驻点是否为极值点。如果是，指出是极大值点还是极小值点。

解答

首先求一阶偏导数：
\[f_x'(x, y) = 2x - 4, \quad f_y'(x, y) = 2y - 6.\]
令偏导数为零，解方程组：
\[\begin{cases} 2x - 4 = 0 \\ 2y - 6 = 0 \end{cases} \Rightarrow x = 2, \quad y = 3.\]
因此，驻点为 $(2, 3)$。
计算二阶偏导数：
\[A = f_{xx}''(x, y) = 2, \quad B = f_{xy}''(x, y) = 0, \quad C = f_{yy}''(x, y) = 2.\]
在点 $(2, 3)$ 处，$A = 2$, $B = 0$, $C = 2$。
计算判别式：
\[AC - B^2 = 2 \times 2 - 0^2 = 4 > 0.\]
由于 $A = 2 > 0$，点 $(2, 3)$ 是极小值点。极小值为 $f(2, 3) = 2^2 + 3^2 - 4 \times 2 - 6 \times 3 + 13 = 0$。

例题2

求函数 $f(x, y) = x^3 + y^3 - 3xy$ 的驻点，并判断这些驻点是否为极值点。如果是，指出是极大值点还是极小值点。

解答

求一阶偏导数：
\[f_x'(x, y) = 3x^2 - 3y, \quad f_y'(x, y) = 3y^2 - 3x.\]
令偏导数为零，解方程组：
\[\begin{cases} 3x^2 - 3y = 0 \\ 3y^2 - 3x = 0 \end{cases} \Rightarrow x^2 = y, \quad y^2 = x.\]
代入 $y = x^2$ 到第二式：$(x^2)^2 = x \Rightarrow x^4 - x = 0 \Rightarrow x(x^3 - 1) = 0$，解得 $x = 0$ 或 $x = 1$。对应地，$y = 0$ 或 $y = 1$。因此，驻点为 $(0, 0)$ 和 $(1, 1)$。
计算二阶偏导数：
\[A = f_{xx}''(x, y) = 6x, \quad B = f_{xy}''(x, y) = -3, \quad C = f_{yy}''(x, y) = 6y.\]
- 在点 $(0, 0)$：$A = 0$, $B = -3$, $C = 0$，判别式 $AC - B^2 = 0 \times 0 - (-3)^2 = -9 < 0$，故 $(0, 0)$ 不是极值点。
- 在点 $(1, 1)$：$A = 6$, $B = -3$, $C = 6$，判别式 $AC - B^2 = 6 \times 6 - (-3)^2 = 36 - 9 = 27 > 0$，且 $A = 6 > 0$，故 $(1, 1)$ 是极小值点。极小值为 $f(1, 1) = 1 + 1 - 3 = -1$。

例题3

设函数 $f(x, y) = xy$ 在条件 $\varphi(x, y) = x + y - 1 = 0$ 下求极值点，并使用拉格朗日乘数法求解。

解答

构造拉格朗日函数： \[L(x, y, \lambda) = xy + \lambda(x + y - 1).\]
求偏导数并令为零： \[\begin{cases} \frac{\partial L}{\partial x} = y + \lambda = 0 \\ \frac{\partial L}{\partial y} = x + \lambda = 0 \\ \frac{\partial L}{\partial \lambda} = x + y - 1 = 0 \end{cases}\]
解方程组：由前两式得 $y = -\lambda$, $x = -\lambda$，代入第三式：$-\lambda - \lambda - 1 = 0 \Rightarrow -2\lambda = 1 \Rightarrow \lambda = -\frac{1}{2}$。从而 $x = \frac{1}{2}$, $y = \frac{1}{2}$。
因此，条件极值点为 $\left( \frac{1}{2}, \frac{1}{2} \right)$。在该点，$f\left( \frac{1}{2}, \frac{1}{2} \right) = \frac{1}{4}$。通过进一步分析（如比较边界值），可确认这是极大值点。

例题4

设函数 $f(x, y) = x^2 + y^2$ 在区域 $D = \{(x, y) \mid 0 \le x \le 2, -1 \le y \le 1\}$ 上。验证：尽管 $(0, 0)$ 是 $f(x, y)$ 在 $D$ 内的唯一极值点（极小值点），但它不是 $f(x, y)$ 在 $D$ 上的最小值点。

解答

求一阶偏导数：
\[f_x'(x, y) = 2x, \quad f_y'(x, y) = 2y.\]
令偏导数为零，得 $x = 0$, $y = 0$，即驻点 $(0, 0)$。
计算二阶偏导数：
\[A = f_{xx}''(x, y) = 2, \quad B = f_{xy}''(x, y) = 0, \quad C = f_{yy}''(x, y) = 2.\]
在 $(0, 0)$ 处，判别式 $AC - B^2 = 4 > 0$ 且 $A > 0$，故 $(0, 0)$ 是极小值点，极小值 $f(0, 0) = 0$。
检查区域边界：
- 在点 $(2, -1) \in D$，$f(2, -1) = 4 + 1 = 5 > 0$。
- 在点 $(0, 0)$，$f(0, 0) = 0$。
- 在点 $(0, -1)$，$f(0, -1) = 0 + 1 = 1 > 0$。虽然 $(0, 0)$ 是极小值点，但边界点 $(0, -1)$ 和 $(0, 1)$ 的值均大于 0，且 $f(x, y) \ge 0$ 在 $D$ 上恒成立。实际上，最小值在 $(0, 0)$ 处取得，值为 0。但若修改函数为 $f(x, y) = x^2 + y^2 - 2x$，则类似例题可构造反例，说明唯一极值点不一定是最值点。本题中，$(0, 0)$ 确为最小值点，但通过此例强调需全面检查边界。