七、一元函数积分学的几何应用

（一）平面图形的面积

1. 直角坐标系中的平面图形的面积

（1）设 $f(x),g(x)$ 在 $[a,b]$ 连续，则由曲线 $y = f(x),y = g(x)$ 及直线 $x = a,x = b(a < b)$ 所围成的区域 $D$ 的面积为 $S = \int_{a}^{b}|f(x) - g(x)|\mathrm{d}x$，其中曲线 $y = f(x),y = g(x)(x\in [a,b])$ 可以有有限个交点（见图3.2）。

特别地，若 $f(x)\geqslant g(x)$（$\forall x\in [a,b]$，如图3.3），则 $S = \int_{a}^{b}[f(x) - g(x)]\mathrm{d}x$。

若 $f(x)\geqslant 0,g(x) = 0$（如图3.4），则 $S = \int_{a}^{b}f(x)\mathrm{d}x$。

【注】当 $f(x)\geq g(x)(x\in [a,b])$ 时公式也可从二重积分的计算公式得到（如图3.3）：

\[S = \iint_{D} \mathrm{d}x\mathrm{d}y = \int_{a}^{b} \mathrm{d}x \int_{g(x)}^{f(x)} \mathrm{d}y = \int_{a}^{b} [f(x) - g(x)] \mathrm{d}x.\]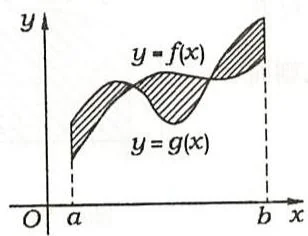

图3.2

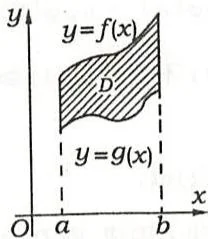
图3.3

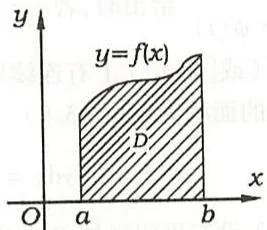
图3.4

（2）设 $\varphi(y),\psi(y)$ 在 $[\alpha,\beta]$ 连续，则由曲线 $x = \varphi(y),x = \psi(y)$ 及直线 $y = \alpha,y = \beta(\alpha < \beta)$ 所围的区域 $D$ 的面积为

\[S = \int_{\alpha}^{\beta} |\varphi(y) - \psi(y)| dy,\]

其中，曲线 $x = \varphi(y)$ 与 $x = \psi(y)$ 在区间 $[\alpha,\beta]$ 上可以有有限个交点（如图3.5）。

【注】当 $\varphi(y)\geqslant \psi(y)(y\in [\alpha,\beta])$ 时公式也可由二重积分的计算公式得到

\[S = \iint_{D} dxdy = \int_{\alpha}^{\beta} dy \int_{\psi(y)}^{\varphi(y)} dx = \int_{\alpha}^{\beta} [\varphi(y) - \psi(y)] dy.\]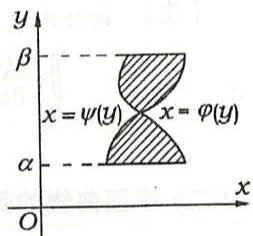

图3.5

2. 极坐标系中的平面图形的面积

（1）设 $r_1(\theta), r_2(\theta)$ 在 $[\alpha, \beta]$ 连续，$r_1(\theta) \leqslant r_2(\theta) (\forall \theta \in [\alpha, \beta])$，则在极坐标系中由曲线 $r = r_1(\theta), r = r_2(\theta)$ 及射线 $\theta = \alpha, \theta = \beta (\alpha < \beta)$ 所围成的区域 $D$ 的面积（如图3.6）为

\[S = \frac{1}{2} \int_{\alpha}^{\beta} \left[ r_{2}^{2}(\theta) - r_{1}^{2}(\theta) \right] d\theta .\]

特别地，当 $r_2(\theta) = r(\theta),r_1(\theta) = 0$ 时（如图3.7），有 $S = \frac{1}{2}\int_{\alpha}^{\beta}r^{2}(\theta)\mathrm{d}\theta$。

【注】以上公式可由二重积分的极坐标变换得

\[S = \iint_{D} dxdy = \iint_{D} r drd\theta = \int_{\alpha}^{\beta} d\theta \int_{r_{1}(\theta)}^{r_{2}(\theta)} r dr = \frac{1}{2} \int_{\alpha}^{\beta} \left[ r_{2}^{2}(\theta) - r_{1}^{2}(\theta) \right] d\theta .\]

（2）设 $\theta_{1}(r), \theta_{2}(r)$ 在 $[a, b]$ 连续，$\theta_{1}(r) \leqslant \theta_{2}(r) (\forall r \in [a, b])$，如图3.8，则在极坐标系中由曲线 $\theta = \theta_{1}(r), \theta = \theta_{2}(r)$ 及圆弧 $r = a, r = b (a < b)$ 所围成的区域 $D$ 的面积为

\[S = \int_{a}^{b} r [\theta_{2}(r) - \theta_{1}(r)] dr.\]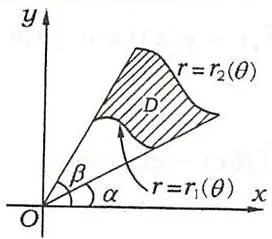

图3.6

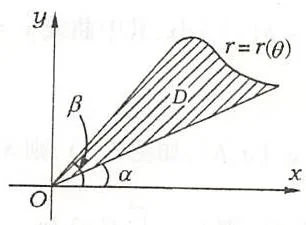
图3.7

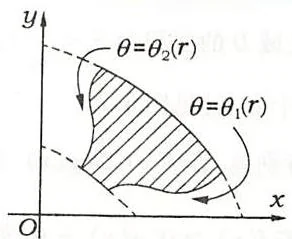
图3.8

3. 边界曲线方程由参数方程给出的平面图形的面积

（1）当曲边梯形的曲边 $y = f(x)(f(x)\geqslant 0,x\in [a,b])$ 由参数方程 $\left\{ \begin{array}{l}x = \varphi(t),\\ y = \psi(t) \end{array} \right.$ 给出时，若 $x = \varphi(t)$ 适合：$\varphi(\alpha) = a$，$\varphi(\beta) = b,\varphi(t)$ 在 $[\alpha,\beta]$（或 $[\beta,\alpha]$）上有连续导数且 $\varphi^{\prime}(t)$ 不变号，$\psi(t)\geqslant 0$ 连续，则曲边梯形的面积为（如图3.9）

\[S = \int_{a}^{b} y dx = \int_{\alpha}^{\beta} \psi(t) \varphi^{\prime}(t) dt.\]

（2）设有界闭区域 $D$ 由分段光滑曲线 $L$ 围成，则 $D$ 的面积为

\[S = \frac{1}{2} \int_{L} - y dx + x dy,\]

其中，$L$ 对 $D$ 来说取正向。

【注】该公式可由格林公式得到：

\[\iint_{D} \left(\frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y} \right) \mathrm{d}x\mathrm{d}y = \oint_{L} P\mathrm{d}x + Q\mathrm{d}y \text{中}, \text{取} P = - y, Q = x \text{即可}.\]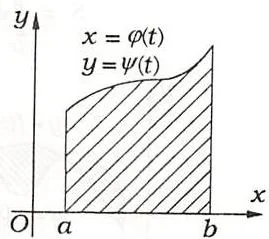

图3.9

（二）平面曲线的弧微分与弧长

设平面曲线弧 $\widehat{AB}$ 由直角坐标方程 $y = f(x)$（$a \leq x \leq b$）给出，则弧微分为 $\mathrm{ds} = \sqrt{1 + f'^2(x)} \, \mathrm{d}x$，弧长为 $s = \int_{a}^{b} \sqrt{1 + f'^2(x)} \, \mathrm{d}x$，其中 $f(x)$ 在 $[a, b]$ 有连续的导数。
设平面曲线弧AB由参数方程 $x = x(t), y = y(t) (\alpha \leqslant t \leqslant \beta)$ 给出，则弧微分为

\[\mathrm{d}s = \sqrt{x^{\prime 2}(t) + y^{\prime 2}(t)} \mathrm{d}t \quad \left((\mathrm{d}s)^{2} = (\mathrm{d}x)^{2} + (\mathrm{d}y)^{2}\right),\]

弧长为 $s = \int_{\alpha}^{\beta}\sqrt{x'^2(t) + y'^2(t)}\mathrm{d}t$，其中 $x(t),y(t)$ 在 $[\alpha,\beta]$ 有连续的导数，$x^{\prime 2}(t) + y^{\prime 2}(t)\neq 0$。

设平面曲线弧AB由极坐标方程 $r = r(\theta)$（$\alpha \leqslant \theta \leqslant \beta$）给出，也就知道了它的参数方程 $x = r(\theta)\cos\theta, y = r(\theta)\sin\theta$（$\alpha \leqslant \theta \leqslant \beta$），则弧微分为 $\mathrm{ds} = \sqrt{r^2(\theta) + r'^2(\theta)}\mathrm{d}\theta$，弧长为 $s = \int_{\alpha}^{\beta}\sqrt{r^2(\theta) + r'^2(\theta)}\mathrm{d}\theta$，其中 $r = r(\theta)$ 在 $[\alpha, \beta]$ 有连续的导数。

【例3.25】求下列平面曲线的弧长：

（I）曲线 $9y^{2} = x(x - 3)^{2}$（$y \geqslant 0$）位于 $x = 0$ 到 $x = 3$ 之间的一段；
（Ⅱ）曲线 $\left(\frac{x}{a}\right)^{\frac{1}{2}} + \left(\frac{y}{b}\right)^{\frac{1}{2}} = 1 (a > 0, b > 0, a \neq b)$。

【解】（I）先求 $y^\prime$ 与 $\sqrt{1 + y^{\prime 2}}$：将 $9y^{2} = x(x - 3)^{2}$ 两边对 $x$ 求导得 $6yy' = (x - 3)(x - 1)$，即 $y^\prime = \frac{1}{6y} (x - 3)(x - 1),\quad \sqrt{1 + y^{\prime 2}} = \frac{1 + x}{2\sqrt{x}}$。因此该段曲线的弧长为

\[s = \int_{0}^{3} \sqrt{1 + y^{\prime 2}} dx = \int_{0}^{3} \frac{1 + x}{2 \sqrt{x}} dx = \frac{1}{2} \int_{0}^{3} \left(\sqrt{x} + \frac{1}{\sqrt{x}}\right) dx = \left. \frac{1}{2} \left(\frac{2}{3} x^{\frac{3}{2}} + 2 x^{\frac{1}{2}}\right) \right|_{0}^{3} = 2 \sqrt{3}.\]

（Ⅱ）先写出曲线的参数方程 $\left\{ \begin{array}{l}x = a\cos^3 t,\\ y = b\sin^3 t, \end{array} \right.$ $t\in [0,2\pi]$，再求

\[\sqrt{x^{\prime 2} + y^{\prime 2}} = 3 |\sin t \cos t| \sqrt{a^{2} \cos^{2} t + b^{2} \sin^{2} t}.\]

于是代公式并由对称性得，该曲线的弧长为

\[\begin{aligned} s &= 4 \int_{0}^{\frac{\pi}{2}} \sqrt{x^{\prime 2}(t) + y^{\prime 2}(t)} dt = 4 \int_{0}^{\frac{\pi}{2}} 3 \sin t \cos t \sqrt{a^{2} \cos^{2} t + b^{2} \sin^{2} t} dt \\ &= 6 \int_{0}^{\frac{\pi}{2}} \sqrt{a^{2} + (b^{2} - a^{2}) \sin^{2} t} d(\sin^{2} t) = \left. \frac{4}{b^{2} - a^{2}} \left[ a^{2} + (b^{2} - a^{2}) \sin^{2} t \right]^{\frac{3}{2}} \right|_{0}^{\frac{\pi}{2}} \\ &= \frac{4}{b^{2} - a^{2}} \left(b^{3} - a^{3}\right). \end{aligned}\]

（三）平面曲线的曲率

1. 平面曲线的曲率、曲率圆与曲率半径的概念

设 $C$ 是光滑曲线（每一点处都有切线且随切点的移动而连续转动）$y = f(x)$。选定一端点作为度量弧 $s$ 的基点。曲线上每一点 $M$ 就对应有弧长为 $s$，点 $M$ 处切线的倾角（如图3.10(a)或3.10(b)）为 $\alpha = \alpha(s)$，称

\[K = \left| \frac{\mathrm{d}\alpha}{\mathrm{d}s} \right|\]

为平面曲线 $C$ 在点 $M$ 的曲率，$\rho = \frac{1}{K}$ 为 $C$ 在点 $M$ 的曲率半径。在点 $M$ 处的曲线 $C$ 的法线上，在凹的一侧取一点 $D$，使 $|DM| = \rho = \frac{1}{K}$，以 $D$ 为圆心，$\rho$ 为半径作圆（图3.10(a)或图3.10(b)），这个圆叫作曲线 $C$ 在点 $M$ 处的曲率圆，圆心 $D$ 叫作曲线 $C$ 在点 $M$ 的曲率中心。

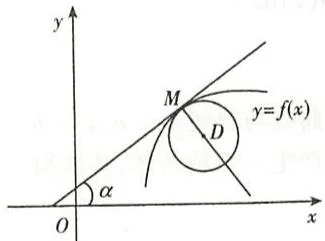
图3.10(a)

图3.10(b)

由此可知，曲线 $C$ 在点 $M$ 处与其曲率圆有相同的切线和曲率，且在点 $M$ 邻近处有相同的凹凸性（参见本章题型训练四，题10）。

【注】对于凸函数，它的凹的一侧即切线的下方一侧（图3.10(a)）；对于凹函数，它的凹的一侧即切线的上方一侧（图3.10(b)）。

2. 曲率的计算公式

（1）设曲线 $C$ 的参数方程为 $x = x(t)$，$y = y(t)$（$t\in [\alpha,\beta]$），则

\[K = \left| \frac{\mathrm{d}\alpha}{\mathrm{d}s} \right| = \frac{|x^{\prime}(t) y^{\prime \prime}(t) - x^{\prime \prime}(t) y^{\prime}(t)|}{[x^{\prime 2}(t) + y^{\prime 2}(t)]^{3 / 2}},\]

其中 $x(t), y(t)$ 在 $[\alpha, \beta]$ 有二阶导数。

（2）设曲线 $C$ 的直角坐标方程为 $y = y(x),y(x)$ 二阶可导，则 $K = \left|\frac{\mathrm{d}\alpha}{\mathrm{d}s}\right| = \frac{|y^{\prime\prime}|}{(1 + y^{\prime 2})^{3 / 2}}$。

【例3.26】求曲线：$x = t - \ln (1 + t^2),y = \arctan t$ 在 $t = 2$ 处的曲率及曲率半径。

利用由参数方程确定的函数的求导法则，得

\[\frac{\mathrm{d}y}{\mathrm{d}x} = \frac{y_{t}^{\prime}}{x_{t}^{\prime}} = \frac{1}{(t - 1)^{2}},\] \[\frac{\mathrm{d}^{2}y}{\mathrm{d}x^{2}} = \left[ \frac{1}{(t - 1)^{2}} \right]^{\prime} \cdot \frac{\mathrm{d}t}{\mathrm{d}x} = \frac{- 2}{(t - 1)^{3}} \cdot \frac{1}{x_{t}^{\prime}} = - \frac{2 (1 + t^{2})}{(t - 1)^{5}},\]

于是所求曲率为 $K = \frac{|y''|}{(1 + y'^2)^{3/2}}\Bigg|_{t=2} = \frac{5}{\sqrt{2}}$。曲率半径 $\rho = \frac{\sqrt{2}}{5}$。

评注：本题也可先求出 $x^{\prime}(t), x^{\prime \prime}(t), y^{\prime}(t), y^{\prime \prime}(t)$，然后直接套公式 $K = \frac{|x'y'' - x''y'|}{(x'^2 + y'^2)^{3/2}}$，这样也能得出结果，但计算量较大。所以要学会”具体问题具体分析”，根据不同的题目选择合适的公式。

（四）空间图形的体积

1. 平行截面面积为已知的立体的体积

设空间某立体由一曲面和垂直于 $z$ 轴的二平面 $z = \alpha, z = \beta$ 围成 $(\alpha < \beta)$，如果过 $z$ 轴上任一点 $z(\alpha \leqslant z \leqslant \beta)$ 且垂直于 $z$ 轴的平面截立体所得的截面面积 $S(z)$ 是已知的连续函数，则该立体的体积（见图3.11）为

\[V = \int_{\alpha}^{\beta} S(z) dz.\]

【注】该立体是空间 $Oxyz$ 中的一个有界闭区域记为 $\

练习题

例题1

题目内容
求由曲线 $y = x^2$ 与 $y = \sqrt{x}$ 所围成的平面图形的面积。

题目解答
首先，求两曲线的交点：

\[x^2 = \sqrt{x} \Rightarrow x^4 = x \Rightarrow x(x^3 - 1) = 0 \Rightarrow x = 0, 1.\]

在区间 $[0, 1]$ 上，$\sqrt{x} \geq x^2$，因此面积为：

\[S = \int_{0}^{1} (\sqrt{x} - x^2) \, dx = \left[ \frac{2}{3}x^{3/2} - \frac{1}{3}x^3 \right]_{0}^{1} = \frac{2}{3} - \frac{1}{3} = \frac{1}{3}.\]

例题2

题目内容
求曲线 $y = \ln x$ 从 $x = 1$ 到 $x = e$ 的弧长。

题目解答
弧长公式为 $s = \int_{a}^{b} \sqrt{1 + (y')^2} \, dx$。
计算导数：$y' = \frac{1}{x}$，则

\[s = \int_{1}^{e} \sqrt{1 + \frac{1}{x^2}} \, dx = \int_{1}^{e} \frac{\sqrt{x^2 + 1}}{x} \, dx.\]

令 $x = \tan t$，则 $dx = \sec^2 t \, dt$，当 $x = 1$ 时 $t = \frac{\pi}{4}$，当 $x = e$ 时 $t = \arctan e$。
积分变为：

\[s = \int_{\pi/4}^{\arctan e} \frac{\sec t}{\tan t} \cdot \sec^2 t \, dt = \int_{\pi/4}^{\arctan e} \csc t \sec t \, dt.\]

利用恒等式 $\csc t \sec t = \frac{1}{\sin t \cos t} = 2 \csc 2t$，得

\[s = 2 \int_{\pi/4}^{\arctan e} \csc 2t \, dt = \left[ -\ln |\csc 2t + \cot 2t| \right]_{\pi/4}^{\arctan e}.\]

代入上下限计算即可（具体数值略）。

例题3

题目内容
求曲线 $y = x^3$ 在点 $(1, 1)$ 处的曲率及曲率半径。

题目解答
曲率公式为 $K = \frac{|y''|}{(1 + y'^2)^{3/2}}$。
计算导数：$y' = 3x^2$, $y'' = 6x$。
在点 $(1, 1)$ 处，$y' = 3$, $y'' = 6$，故

\[K = \frac{6}{(1 + 9)^{3/2}} = \frac{6}{10^{3/2}} = \frac{6}{10\sqrt{10}} = \frac{3}{5\sqrt{10}}.\]

曲率半径为 $\rho = \frac{1}{K} = \frac{5\sqrt{10}}{3}$.

例题4

题目内容
求由曲线 $y = \sin x$ ($0 \leq x \leq \pi$) 绕 $x$-轴旋转一周所成旋转体的体积。

题目解答
旋转体体积公式为 $V = \pi \int_{a}^{b} [f(x)]^2 \, dx$。

\[V = \pi \int_{0}^{\pi} \sin^2 x \, dx = \pi \int_{0}^{\pi} \frac{1 - \cos 2x}{2} \, dx = \frac{\pi}{2} \left[ x - \frac{\sin 2x}{2} \right]_{0}^{\pi} = \frac{\pi}{2} \cdot \pi = \frac{\pi^2}{2}.\]

例题5

题目内容
求曲线 $y = \sqrt{x}$ ($1 \leq x \leq 4$) 绕 $x$-轴旋转一周所成旋转曲面的侧面积。

题目解答
旋转曲面侧面积公式为 $S = 2\pi \int_{a}^{b} y \sqrt{1 + (y')^2} \, dx$。
计算导数：$y' = \frac{1}{2\sqrt{x}}$，则

\[S = 2\pi \int_{1}^{4} \sqrt{x} \cdot \sqrt{1 + \frac{1}{4x}} \, dx = 2\pi \int_{1}^{4} \sqrt{x + \frac{1}{4}} \, dx.\]

令 $u = x + \frac{1}{4}$，则 $du = dx$，积分限变为 $\frac{5}{4}$ 到 $\frac{17}{4}$。

\[S = 2\pi \int_{5/4}^{17/4} u^{1/2} \, du = 2\pi \cdot \frac{2}{3} \left[ u^{3/2} \right]_{5/4}^{17/4} = \frac{4\pi}{3} \left( \left( \frac{17}{4} \right)^{3/2} - \left( \frac{5}{4} \right)^{3/2} \right).\]

化简得 $S = \frac{\pi}{6} (17\sqrt{17} - 5\sqrt{5})$.

例题6

题目内容
求由极坐标方程 $r = 2(1 + \cos \theta)$ 所围图形的面积。

题目解答
极坐标下面积公式为 $S = \frac{1}{2} \int_{\alpha}^{\beta} r^2 \, d\theta$。
由于图形对称，取 $\theta \in [0, 2\pi]$：

\[S = \frac{1}{2} \int_{0}^{2\pi} [2(1 + \cos \theta)]^2 \, d\theta = 2 \int_{0}^{2\pi} (1 + 2\cos \theta + \cos^2 \theta) \, d\theta.\]

利用 $\cos^2 \theta = \frac{1 + \cos 2\theta}{2}$，得

\[S = 2 \int_{0}^{2\pi} \left( \frac{3}{2} + 2\cos \theta + \frac{1}{2} \cos 2\theta \right) d\theta = 2 \left[ \frac{3}{2} \theta + 2\sin \theta + \frac{1}{4} \sin 2\theta \right]_{0}^{2\pi} = 2 \cdot 3\pi = 6\pi.\]