七、多元函数的最大值与最小值问题

（一）极值（最值）问题的提法

1. 简单极值（最值）问题（或普通极值问题）

求二元函数 \(z = f(x,y)\) 在 \(Oxy\) 平面上某区域 \(D\) 上的最大值或最小值。

求三元函数 \(u = f(x,y,z)\) 在 \(Oxyz\) 空间中某区域 \(\Omega\) 上的最大值或最小值。

2. 条件极值（最值）问题

求二元函数 \(z = f(x,y)\) 在条件 \(\varphi (x,y) = 0\) 下的最大值或最小值问题。

求三元函数 \(u = f(x,y,z)\) 在条件 \(\varphi (x,y,z) = 0\) 下或条件 \(\varphi (x,y,z) = 0,\psi (x,y,z) = 0\) 下的最大值或最小值问题。

（二）求二元函数或三元函数的简单极值问题

1. 有界闭区域上的最值问题

设 \(z = f(x, y)\) 在平面有界闭区域 \(D\) 上连续，则 \(f(x, y)\) 在 \(D\) 存在最大值 \(M\) 和最小值 \(m\)，它们或在 \(D\) 内满足 \(\frac{\partial f}{\partial x} = 0, \frac{\partial f}{\partial y} = 0\) 的点（即 \(f(x, y)\) 的驻点）处达到，或在偏导数不存在的点处达到，或在 \(D\) 的边界点上达到。因此，求连续函数 \(f(x, y)\) 在有界闭区域 \(D\) 上的最值的步骤如下：

第一步，求出 \(f(x, y)\) 在 \(D\) 内可能取得极值点（驻点和一阶偏导数不存在的点）的函数值。

第二步，求出 \(f(x,y)\) 在 \(D\) 的边界上的最大、最小值。

第三步，将上面求得各函数值进行比较，最大（小）者为最大（小）值。

【注】对三元函数有类似结论。

2. 开区域上的最值问题

设 \(z = f(x, y)\) 在开区域 \(D\) 内可偏导，且根据实际问题可知它在 \(D\) 内有最大值或最小值，则只需在满足 \(\frac{\partial f}{\partial x} = 0, \frac{\partial f}{\partial y} = 0\) 的点中找到 \(f(x, y)\) 的最大值点或最小值点。

【例8.11】

求函数 \(z = x^{2}y(4 - x - y)\) 在由直线 \(x + y = 6\)，\(x\) 轴和 \(y\) 轴所围成的区域 \(D\) 上的最大值与最小值。

【解】区域 \(D\) 如图8.1所示，它是有界闭区域。\(z(x,y)\) 在 \(D\) 上连续，所以在 \(D\) 上一定有最大值与最小值，它或在 \(D\) 内的驻点达到，或在 \(D\) 的边界上达到。

为求 \(D\) 内驻点，先求：

\[\frac {\partial z}{\partial x} = 2 x y (4 - x - y) - x ^ {2} y = x y (8 - 3 x - 2 y),\] \[\frac {\partial z}{\partial y} = x ^ {2} (4 - x - y) - x ^ {2} y = x ^ {2} (4 - x - 2 y).\]

再解方程组 \(\left\{ \begin{array}{l} 3x + 2y = 8, \\ x + 2y = 4, \end{array} \right.\) 得 \(z(x,y)\) 在 \(D\) 内的唯一驻点 \((x,y) = (2,1)\) 且 \(z(2,1) = 4\)。

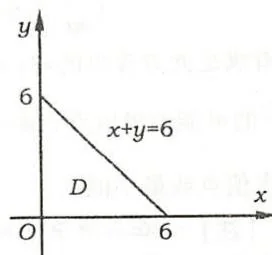
图8.1

在 \(D\) 的边界 \(y = 0,0\leqslant x\leqslant 6\) 或 \(x = 0,0\leqslant y\leqslant 6\) 上 \(z(x,y) = 0\)。

在边界 \(x + y = 6\)（\(0 \leqslant x \leqslant 6\)）上将 \(y = 6 - x\) 代入得 \(z(x, y) = x^2(6 - x)(-2) = 2(x^3 - 6x^2)\)，\(0 \leqslant x \leqslant 6\)。令 \(h(x) = 2(x^3 - 6x^2)\)，则 \(h'(x) = 6(x^2 - 4x)\)，\(h'(4) = 0\)，\(h(0) = 0\)，\(h(4) = -64\)，\(h(6) = 0\)，即 \(z(x, y)\) 在边界 \(x + y = 6\)（\(0 \leqslant x \leqslant 6\)）上的最大值为0，最小值为-64。

因此，\(\max_{D}z(x,y) = 4,\min_{D}z(x,y) = -64\)。

（三）求二元函数或三元函数的条件极值问题

1. 求函数 \(z = f(x, y)\) 在条件 \(\varphi(x, y) = 0\) 下的最大值或最小值

方法 \(1^{\circ}\) 化为无条件极值（最值）。若从条件 \(\varphi (x,y) = 0\) 中可解出 \(y = y(x)\) 或 \(x = x(y)\)，把它代入 \(z = f(x,y)\)，则可化为相应一元函数的最值问题。

方法 \(2^{\circ}\) 拉格朗日乘数法。首先构造辅助函数（称为拉格朗日函数）\(F(x, y, \lambda) = f(x, y) + \lambda \varphi(x, y)\)，然后求解方程组：

\[\left\{ \begin{array}{l} \frac {\partial F}{\partial x} = \frac {\partial f}{\partial x} + \lambda \frac {\partial \varphi}{\partial x} = 0, \\ \frac {\partial F}{\partial y} = \frac {\partial f}{\partial y} + \lambda \frac {\partial \varphi}{\partial y} = 0, \\ \frac {\partial F}{\partial \lambda} = \varphi (x, y) = 0. \end{array} \right. \tag {8.10}\]

所有满足此方程组的解 \((x,y,\lambda)\) 中 \((x,y)\) 是 \(f(x,y)\) 在条件 \(\varphi (x,y) = 0\) 下的可能的极值点，最后比较这些可能极值点（若曲线 \(\varphi (x,y) = 0\) 含端点，还需考察其端点）的函数值得出最大值点或最小值点。

【注】

① 判别条件极值时千万不能用无条件极值常用的方法来判别。
② 这个方法可推广到求三元函数 \(u = f(x, y, z)\) 在条件 \(\varphi(x, y, z) = 0\) 下或条件 \(\varphi(x, y, z) = 0\)，\(\psi(x, y, z) = 0\) 下的最大值或最小值。

2. 求函数 \(u = f(x,y,z)\) 在条件 \(\varphi (x,y,z) = 0,\psi (x,y,z) = 0\) 下的最大值或最小值

拉格朗日乘数法：首先构造辅助函数 \(F(x,y,z,\lambda ,\mu) = f(x,y,z) + \lambda \varphi (x,y,z) + \mu \psi (x,y,z)\)，然后求解方程组：

\[\left\{ \begin{array}{l} \frac {\partial F}{\partial x} = \frac {\partial f}{\partial x} + \lambda \frac {\partial \varphi}{\partial x} + \mu \frac {\partial \psi}{\partial x} = 0, \\ \frac {\partial F}{\partial y} = \frac {\partial f}{\partial y} + \lambda \frac {\partial \varphi}{\partial y} + \mu \frac {\partial \psi}{\partial y} = 0, \\ \frac {\partial F}{\partial z} = \frac {\partial f}{\partial z} + \lambda \frac {\partial \varphi}{\partial z} + \mu \frac {\partial \psi}{\partial z} = 0, \\ \frac {\partial F}{\partial \lambda} = \varphi (x, y, z) = 0, \\ \frac {\partial F}{\partial \mu} = \psi (x, y, z) = 0. \end{array} \right. \tag {8.11}\]

所有满足此方程组的解 \((x,y,z,\lambda ,\mu)\) 中 \((x,y,z)\) 是 \(u = f(x,y,z)\) 在条件 \(\varphi (x,y,z) = 0\) 与 \(\psi (x,y,z) = 0\) 下的可能的极值点。最后由可能的极值点中（若曲线 \(\left\{ \begin{array}{ll}\varphi (x,y,z) = 0\\ \psi (x,y,z) = 0 \end{array} \right.\) 含端点，还需考察其端点）求得最大值点或最小值点。

【注】在求解条件极值的应用问题时，常可从问题的实际意义知道所求的最大值或最小值存在，若拉格朗日函数又只有一个驻点，这时可以断言所求的最大值或最小值就在这个驻点处达到。

【例8.12】

已知平面曲线 \(Ax^{2} + 2Bxy + Cy^{2} = 1\)（\(C > 0, AC - B^{2} > 0\)）为中心在原点的椭圆，求它的面积。

【分析】只需求椭圆的半长轴 \(a\) 与半短轴 \(b\)，它们分别是椭圆上的点到中心（原点）的距离的最大值与最小值。因此，归结为求解条件极值问题。

【解】椭圆上点 \((x, y)\) 到原点的距离平方为 \(d^2 = x^2 + y^2\)，条件为 \(Ax^2 + 2Bxy + Cy^2 - 1 = 0\)。

令 \(F(x,y,\lambda) = x^{2} + y^{2} - \lambda (Ax^{2} + 2Bxy + Cy^{2} - 1)\)，解方程组：

\[\left\{ \begin{array}{l} F _ {x} ^ {\prime} = (2 - 2 A \lambda) x - 2 B \lambda y = 0, \\ F _ {y} ^ {\prime} = - 2 B \lambda x + (2 - 2 C \lambda) y = 0, \\ F _ {\lambda} ^ {\prime} = - \left(A x ^ {2} + 2 B x y + C y ^ {2} - 1\right) = 0, \end{array} \right. \tag {①}\]

将①式乘 \(x\)，②式乘 \(y\)，然后两式相加得：

\[\left[ (1 - A \lambda) x ^ {2} - B \lambda x y \right] + \left[ - B \lambda x y + (1 - C \lambda) y ^ {2} \right] = 0,\]

即 \(x^{2} + y^{2} = \lambda (Ax^{2} + 2Bxy + Cy^{2}) = \lambda\)，

于是可得 \(d = \sqrt{\lambda}\)。

从直观知道，函数 \(d^2\) 的条件最大值点与最小值点是存在的，其坐标不同时为零，即联立方程组 \(F_{x}^{\prime} = 0, F_{y}^{\prime} = 0\) 有非零解，其系数行列式应为零，即：

\[\left| \begin{array}{l l} {1 - A \lambda} & {- B \lambda} \\ {- B \lambda} & {1 - C \lambda} \end{array} \right| = 0, \quad \text {亦即} \quad \lambda^ {2} - \frac {A + C}{A C - B ^ {2}} \lambda + \frac {1}{A C - B ^ {2}} = 0.\]

该方程一定有两个根 \(\lambda_1, \lambda_2\)，它们分别对应 \(d^2\) 的最大值与最小值。因此，椭圆的面积为：

\[S = \pi \sqrt {\lambda_ {1} \lambda_ {2}} = \frac {\pi}{\sqrt {A C - B ^ {2}}}.\]

练习题

例题1

求函数 \(f(x,y) = x^2 + y^2 - 2x - 4y\) 在闭区域 \(D = \{(x,y) \mid x^2 + y^2 \leq 9\}\) 上的最大值和最小值。

解答

求内部驻点：
计算偏导数：
\[\frac{\partial f}{\partial x} = 2x - 2, \quad \frac{\partial f}{\partial y} = 2y - 4\]
令偏导数为零，解得驻点 \((1, 2)\)，且 \(f(1,2) = 1 + 4 - 2 - 8 = -5\)。
求边界极值：
边界为 \(x^2 + y^2 = 9\)。使用拉格朗日乘数法，设
\[F(x,y,\lambda) = x^2 + y^2 - 2x - 4y + \lambda(x^2 + y^2 - 9)\]
解方程组：
\[\begin{cases} \frac{\partial F}{\partial x} = 2x - 2 + 2\lambda x = 0 \\ \frac{\partial F}{\partial y} = 2y - 4 + 2\lambda y = 0 \\ \frac{\partial F}{\partial \lambda} = x^2 + y^2 - 9 = 0 \end{cases}\]
由前两式得 \(x = \frac{1}{1+\lambda}, \quad y = \frac{2}{1+\lambda}\)。代入第三式：
\[\left(\frac{1}{1+\lambda}\right)^2 + \left(\frac{2}{1+\lambda}\right)^2 = 9 \implies \frac{5}{(1+\lambda)^2} = 9 \implies 1+\lambda = \pm \frac{\sqrt{5}}{3}\]
对应点 \(\left(\frac{3}{\sqrt{5}}, \frac{6}{\sqrt{5}}\right)\) 和 \(\left(-\frac{3}{\sqrt{5}}, -\frac{6}{\sqrt{5}}\right)\)，函数值分别为：
\[f\left(\frac{3}{\sqrt{5}}, \frac{6}{\sqrt{5}}\right) = \frac{45}{5} - \frac{6}{\sqrt{5}} - \frac{24}{\sqrt{5}} = 9 - 6\sqrt{5}\] \[f\left(-\frac{3}{\sqrt{5}}, -\frac{6}{\sqrt{5}}\right) = \frac{45}{5} + \frac{6}{\sqrt{5}} + \frac{24}{\sqrt{5}} = 9 + 6\sqrt{5}\]
比较函数值：
- 内部驻点：\(f(1,2) = -5\)
- 边界点：\(9 - 6\sqrt{5} \approx -4.42, \quad 9 + 6\sqrt{5} \approx 22.42\)
  最大值为 \(9 + 6\sqrt{5}\)，最小值为 \(-5\)。

例题2

求函数 \(f(x,y,z) = x + 2y + 3z\) 在条件 \(x^2 + y^2 + z^2 = 14\) 下的最大值和最小值。

解答
使用拉格朗日乘数法，设

\[F(x,y,z,\lambda) = x + 2y + 3z + \lambda(x^2 + y^2 + z^2 - 14)\]

解方程组：

\[\begin{cases} \frac{\partial F}{\partial x} = 1 + 2\lambda x = 0 \\ \frac{\partial F}{\partial y} = 2 + 2\lambda y = 0 \\ \frac{\partial F}{\partial z} = 3 + 2\lambda z = 0 \\ \frac{\partial F}{\partial \lambda} = x^2 + y^2 + z^2 - 14 = 0 \end{cases}\]

由前三式得 \(x = -\frac{1}{2\lambda}, \quad y = -\frac{1}{\lambda}, \quad z = -\frac{3}{2\lambda}\)。代入第四式：

\[\frac{1}{4\lambda^2} + \frac{1}{\lambda^2} + \frac{9}{4\lambda^2} = 14 \implies \frac{14}{4\lambda^2} = 14 \implies \lambda^2 = \frac{1}{4} \implies \lambda = \pm \frac{1}{2}\]

当 \(\lambda = \frac{1}{2}\)，得 \(x = -1, y = -2, z = -3\)，\(f = -1 -4 -9 = -14\)
当 \(\lambda = -\frac{1}{2}\)，得 \(x = 1, y = 2, z = 3\)，\(f = 1 + 4 + 9 = 14\)
最大值为 \(14\)，最小值为 \(-14\)。

例题3

求函数 \(f(x,y) = xy\) 在条件 \(x^2 + y^2 = 8\) 下的最大值和最小值。

解答
使用拉格朗日乘数法，设

\[F(x,y,\lambda) = xy + \lambda(x^2 + y^2 - 8)\]

解方程组：

\[\begin{cases} \frac{\partial F}{\partial x} = y + 2\lambda x = 0 \\ \frac{\partial F}{\partial y} = x + 2\lambda y = 0 \\ \frac{\partial F}{\partial \lambda} = x^2 + y^2 - 8 = 0 \end{cases}\]

由前两式相减得 \(y - x + 2\lambda(x - y) = 0 \implies (y - x)(1 - 2\lambda) = 0\)。

若 \(y = x\)，代入第三式得 \(2x^2 = 8 \implies x = \pm 2\)，对应点 \((2,2), (-2,-2)\)，\(f = 4\)
若 \(\lambda = \frac{1}{2}\)，由第一式 \(y + x = 0 \implies y = -x\)，代入第三式得 \(2x^2 = 8 \implies x = \pm 2\)，对应点 \((2,-2), (-2,2)\)，\(f = -4\)
最大值为 \(4\)，最小值为 \(-4\)。

例题4

求函数 \(f(x,y) = x^2 + 2y^2\) 在区域 \(D = \{(x,y) \mid x^2 + y^2 \leq 4\}\) 上的最大值和最小值。

解答

求内部驻点：
\[\frac{\partial f}{\partial x} = 2x = 0, \quad \frac{\partial f}{\partial y} = 4y = 0\]
解得驻点 \((0,0)\)，\(f(0,0) = 0\)。
求边界极值：
边界为 \(x^2 + y^2 = 4\)。设
\[F(x,y,\lambda) = x^2 + 2y^2 + \lambda(x^2 + y^2 - 4)\]
解方程组：
\[\begin{cases} \frac{\partial F}{\partial x} = 2x + 2\lambda x = 0 \\ \frac{\partial F}{\partial y} = 4y + 2\lambda y = 0 \\ \frac{\partial F}{\partial \lambda} = x^2 + y^2 - 4 = 0 \end{cases}\]
由第一式 \(2x(1+\lambda) = 0\)，得 \(x = 0\) 或 \(\lambda = -1\)。
- 若 \(x = 0\)，由第三式 \(y^2 = 4 \implies y = \pm 2\)，\(f = 8\)
- 若 \(\lambda = -1\)，由第二式 \(4y - 2y = 0 \implies y = 0\)，由第三式 \(x^2 = 4 \implies x = \pm 2\)，\(f = 4\)
比较函数值：
- 内部：\(0\)
- 边界：\(4, 8\)
  最大值为 \(8\)，最小值为 \(0\)。