三、向量的运算

（一）定义与计算公式

设 $\boldsymbol{a}_{j} = x_{j}\boldsymbol{i} + y_{j}\boldsymbol{j} + z_{j}\boldsymbol{k} = \{x_{j},y_{j},z_{j}\},\quad j = 1,2,3.$

加法由平行四边形法则或三角形法则给出，用坐标作运算则有

\[\boldsymbol{a}_{1} + \boldsymbol{a}_{2} = \{x_{1} + x_{2}, y_{1} + y_{2}, z_{1} + z_{2}\}. \tag{7.1}\]

数乘向量 $\lambda \boldsymbol{a}$ 是一个向量，其模 $|\lambda \boldsymbol{a}| = |\lambda||\boldsymbol{a}|$，而方向规定为：若 $\lambda > 0$，则 $\lambda \boldsymbol{a}$ 与 $\boldsymbol{a}$ 同向，若 $\lambda < 0$，则 $\lambda \boldsymbol{a}$ 与 $\boldsymbol{a}$ 反向。用坐标作运算为：若 $\boldsymbol{a} = \{x, y, z\}$，则

\[\lambda \boldsymbol{a} = \{\lambda x, \lambda y, \lambda z\}. \tag{7.2}\]

【注】$\lambda \boldsymbol{0} = \boldsymbol{0},\quad 0\boldsymbol{a} = \boldsymbol{0}.$

向量的数量积（点积，内积） $\boldsymbol{a}_1 \cdot \boldsymbol{a}_2$ 是一个数，规定为 $\boldsymbol{a}_1 \cdot \boldsymbol{a}_2 = |\boldsymbol{a}_1||\boldsymbol{a}_2|\cos \theta$，其中 $\theta$ 是 $\boldsymbol{a}_1$ 与 $\boldsymbol{a}_2$ 的夹角。用坐标作运算则有

\[\boldsymbol{a}_{1} \cdot \boldsymbol{a}_{2} = x_{1}x_{2} + y_{1}y_{2} + z_{1}z_{2}, \tag{7.3}\]

两个向量的夹角是指不超过 $\pi$ 的那个角。

向量的向量积（叉积，外积） $\boldsymbol{a}_1 \times \boldsymbol{a}_2$ 是一个向量，其模 $|\boldsymbol{a}_1 \times \boldsymbol{a}_2| = |\boldsymbol{a}_1||\boldsymbol{a}_2|\sin \theta$，其中 $\theta$ 是 $\boldsymbol{a}_1,\boldsymbol{a}_2$ 的夹角，其方向规定为与 $\boldsymbol{a}_1,\boldsymbol{a}_2$ 都垂直且 $\boldsymbol{a}_1,\boldsymbol{a}_2,\boldsymbol{a}_1 \times \boldsymbol{a}_2$ 符合右手系。用坐标作运算为

\[\boldsymbol{a}_{1} \times \boldsymbol{a}_{2} = \left| \begin{array}{ccc} \boldsymbol{i} & \boldsymbol{j} & \boldsymbol{k} \\ x_{1} & y_{1} & z_{1} \\ x_{2} & y_{2} & z_{2} \end{array} \right|. \tag{7.4}\]

混合积 三个向量 $\boldsymbol{a}_1,\boldsymbol{a}_2,\boldsymbol{a}_3$ 的混合积 $(\boldsymbol{a}_{1},\boldsymbol{a}_{2},\boldsymbol{a}_{3})$ 是一个数，规定为 $(\boldsymbol{a}_{1},\boldsymbol{a}_{2},\boldsymbol{a}_{3}) = (\boldsymbol{a}_{1} \times \boldsymbol{a}_{2}) \cdot \boldsymbol{a}_{3}$。用坐标作运算就是

\[(\boldsymbol{a}_{1}, \boldsymbol{a}_{2}, \boldsymbol{a}_{3}) = \left| \begin{array}{ccc} x_{1} & y_{1} & z_{1} \\ x_{2} & y_{2} & z_{2} \\ x_{3} & y_{3} & z_{3} \end{array} \right|. \tag{7.5}\]

（二）运算法则

加法与数乘

\[\begin{aligned} \boldsymbol{a} + \boldsymbol{b} &= \boldsymbol{b} + \boldsymbol{a}, \\ (\boldsymbol{a} + \boldsymbol{b}) + \boldsymbol{c} &= \boldsymbol{a} + (\boldsymbol{b} + \boldsymbol{c}), \\ \lambda (\mu \boldsymbol{a}) &= (\lambda \mu) \boldsymbol{a}, \\ (\lambda + \mu) \boldsymbol{a} &= \lambda \boldsymbol{a} + \mu \boldsymbol{a}, \\ \lambda (\boldsymbol{a} + \boldsymbol{b}) &= \lambda \boldsymbol{a} + \lambda \boldsymbol{b}, \\ \boldsymbol{0} + \boldsymbol{a} &= \boldsymbol{a}, \\ \boldsymbol{a} + (-\boldsymbol{a}) &= \boldsymbol{0}, \\ 1 \cdot \boldsymbol{a} &= \boldsymbol{a}. \end{aligned}\]

数量积

\[\boldsymbol{a} \cdot \boldsymbol{b} = \boldsymbol{b} \cdot \boldsymbol{a}, \quad (\boldsymbol{a} + \boldsymbol{b}) \cdot \boldsymbol{c} = \boldsymbol{a} \cdot \boldsymbol{c} + \boldsymbol{b} \cdot \boldsymbol{c}, \quad (\lambda \boldsymbol{a}) \cdot \boldsymbol{b} = \lambda (\boldsymbol{a} \cdot \boldsymbol{b}). \tag{7.7}\]

向量积

\[\begin{aligned} \boldsymbol{a} \times \boldsymbol{b} &= -\boldsymbol{b} \times \boldsymbol{a}, \\ (\lambda \boldsymbol{a}) \times \boldsymbol{b} &= \lambda (\boldsymbol{a} \times \boldsymbol{b}), \\ \boldsymbol{a} \times (\boldsymbol{b} + \boldsymbol{c}) &= \boldsymbol{a} \times \boldsymbol{b} + \boldsymbol{a} \times \boldsymbol{c}, \\ \boldsymbol{a} \times \boldsymbol{a} &= \boldsymbol{0}. \end{aligned}\]

混合积

\[\begin{aligned} (\boldsymbol{a}, \boldsymbol{b}, \boldsymbol{c}) &= (\boldsymbol{b}, \boldsymbol{c}, \boldsymbol{a}) = (\boldsymbol{c}, \boldsymbol{a}, \boldsymbol{b}), \\ (\boldsymbol{a}, \boldsymbol{a}, \boldsymbol{b}) &= (\boldsymbol{a}, \boldsymbol{b}, \boldsymbol{a}) = (\boldsymbol{a}, \boldsymbol{b}, \boldsymbol{b}) = \boldsymbol{0}, \\ (\boldsymbol{a}, \boldsymbol{b}, \boldsymbol{c}) &= -(\boldsymbol{b}, \boldsymbol{a}, \boldsymbol{c}), \\ (\lambda \boldsymbol{a}, \boldsymbol{b}, \boldsymbol{c}) &= \lambda (\boldsymbol{a}, \boldsymbol{b}, \boldsymbol{c}), \tag{7.9} \\ (\boldsymbol{a}_{1} + \boldsymbol{a}_{2}, \boldsymbol{b}, \boldsymbol{c}) &= (\boldsymbol{a}_{1}, \boldsymbol{b}, \boldsymbol{c}) + (\boldsymbol{a}_{2}, \boldsymbol{b}, \boldsymbol{c}). \end{aligned}\]

（三）几何应用

1. 加法与数乘的几何应用

（1）建立坐标系；建立直线方程；建立平面方程。
（2）过点 $P_{0}$，方向向量为 $\boldsymbol{S}$ 的直线的向量方程是 $\boldsymbol{r} - \boldsymbol{r}_{0} = t\boldsymbol{S}$（见图7.1）。
（3）过点 $P_{0}$，与 $\boldsymbol{U}_{1}, \boldsymbol{U}_{2}$（$\boldsymbol{U}_{1}, \boldsymbol{U}_{2}$ 不平行）都平行的平面的向量方程是 $\boldsymbol{r} - \boldsymbol{r}_{0} = t_{1}\boldsymbol{U}_{1} + t_{2}\boldsymbol{U}_{2}$（见图7.2）。

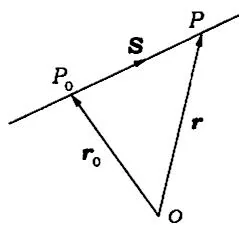
图7.1

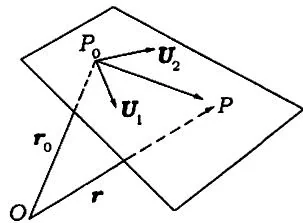
图7.2

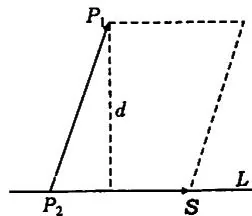
图7.3

（4）设有任意非零向量 $\boldsymbol{a}$，则 $\boldsymbol{a} = |\boldsymbol{a}| \boldsymbol{a}_0$，其中 $\boldsymbol{a}_0$ 是与 $\boldsymbol{a}$ 同方向的单位向量。

2. 数量积的几何应用

（1）求模 $|\boldsymbol{a}| = \sqrt{\boldsymbol{a}^2}$，进而可求两点距离。
（2）求两个向量的夹角 $\theta$，进而可求两条直线、直线与平面、两个平面之间的夹角。
（3）判定垂直：$\boldsymbol{a}_{1} \perp \boldsymbol{a}_{2} \Leftrightarrow \boldsymbol{a}_{1} \cdot \boldsymbol{a}_{2} = 0$，进而可证两条直线、两个平面的垂直关系，以及直线与平面的平行关系。
（4）求点到平面的距离。
（5）建立平面方程（点法式）：$\boldsymbol{n} \cdot (\boldsymbol{r} - \boldsymbol{r}_0) = 0$。

3. 向量积的几何应用

（1）求平行四边形（三角形）面积（以 $\boldsymbol{a}, \boldsymbol{b}$ 为两邻边的平行四边形的面积为 $|\boldsymbol{a} \times \boldsymbol{b}|$），进而可求点到直线的距离（图7.3）

\[d = \frac{|\overrightarrow{P_{0}P_{1}} \times \boldsymbol{S}|}{|\boldsymbol{S}|}. \tag{7.10}\]

（2）求两个平面交线的方向向量 $\boldsymbol{S}$，从而可把直线的一般方程化为直线的标准方程。设这两个平面的法向量分别是 $\boldsymbol{n}_1$ 和 $\boldsymbol{n}_2$，则交线 $L$ 与 $\boldsymbol{n}_1, \boldsymbol{n}_2$ 都要垂直，故可取 $\boldsymbol{S} = \boldsymbol{n}_1 \times \boldsymbol{n}_2$。

（3）判断平行：

\[\begin{aligned} &\boldsymbol{a}_{1} \parallel \boldsymbol{a}_{2} \Leftrightarrow \boldsymbol{a}_{1} \times \boldsymbol{a}_{2} = \boldsymbol{0} \Leftrightarrow \frac{x_{1}}{x_{2}} = \frac{y_{1}}{y_{2}} = \frac{z_{1}}{z_{2}} \quad (\text{坐标成比例}, \boldsymbol{a}_{j} = (x_{j}, y_{j}, z_{j}), j = 1, 2) \\ &\qquad \Leftrightarrow \text{存在实数} \lambda, \text{使得} \boldsymbol{a}_{1} = \lambda \boldsymbol{a}_{2} \text{或} \boldsymbol{a}_{2} = \lambda \boldsymbol{a}_{1}. \end{aligned}\]

4. 混合积的几何应用

（1）判断三个向量（或四个点）是否共面。向量 $\boldsymbol{a}_{1} = \{x_{1}, y_{1}, z_{1}\}$，$\boldsymbol{a}_{2} = \{x_{2}, y_{2}, z_{2}\}$，$\boldsymbol{a}_{3} = \{x_{3}, y_{3}, z_{3}\}$ 共面

\[\Leftrightarrow \quad \text{混合积} (\boldsymbol{a}_{1}, \boldsymbol{a}_{2}, \boldsymbol{a}_{3}) = 0\] \[\Leftrightarrow \quad \left| \begin{array}{ccc} x_{1} & x_{2} & x_{3} \\ y_{1} & y_{2} & y_{3} \\ z_{1} & z_{2} & z_{3} \end{array} \right| = 0\]

$\Leftrightarrow$ 存在不全为零的数 $k_{1}, k_{2}, k_{3}$，使 $k_{1}\boldsymbol{a}_{1} + k_{2}\boldsymbol{a}_{2} + k_{3}\boldsymbol{a}_{3} = \boldsymbol{0}$。

（2）进而可建立平面方程。若 $\boldsymbol{U}_{1} = \{X_{1}, Y_{1}, Z_{1}\}, \boldsymbol{U}_{2} = \{X_{2}, Y_{2}, Z_{2}\}$ 不平行，则过点 $P_{0}(x_{0}, y_{0}, z_{0})$ 与 $\boldsymbol{U}_{1}, \boldsymbol{U}_{2}$ 都平行的平面的方程是 $(\overrightarrow{P_{0}P}, \boldsymbol{U}_{1}, \boldsymbol{U}_{2}) = 0$。用坐标表示，即

\[\left| \begin{array}{ccc} x - x_{0} & y - y_{0} & z - z_{0} \\ X_{1} & Y_{1} & Z_{1} \\ X_{2} & Y_{2} & Z_{2} \end{array} \right| = 0. \tag{7.11}\]

（3）求平行六面体的体积（亦可求四面体的体积）。以 $\boldsymbol{a}, \boldsymbol{b}, \boldsymbol{c}$ 为三条棱的平行六面体的体积是 $|(\boldsymbol{a}, \boldsymbol{b}, \boldsymbol{c})|$。
（4）进而可判断两条直线是否异面并求两条异面直线公垂线的长。设直线 $L_{1},L_{2}$ 分别过点 $P_{1},P_{2}$，其方向向量分别为 $\boldsymbol{U}_{1},\boldsymbol{U}_{2}$，则 $L_{1}$ 与 $L_{2}$ 是异面直线 $\Leftrightarrow (\overrightarrow{P_1P_2},\boldsymbol{U}_1,\boldsymbol{U}_{2}) \neq 0$。

设 $L_{1}, L_{2}$ 是异面直线，过 $L_{1}$ 作平面 $\Pi$ 平行于直线 $L_{2}$，设 $L_{2}$ 在 $\Pi$ 上投影直线为 $QR$，它交 $L_{1}$ 于 $Q$，并设 $Q$ 为 $L_{2}$ 上点 $P$ 在 $\Pi$ 上的投影，$\overline{PQ}$ 就是 $L_{1}$ 与 $L_{2}$ 的公垂线。以 $\boldsymbol{U}_{1}$，

图7.4

$\boldsymbol{U}_{2}, \overrightarrow{P_{1}P_{2}}$ 为棱构造平行六面体，则底面 $\boldsymbol{U}_{1}, \boldsymbol{U}_{2}$ 上的高就是公垂线 $\overline{PQ}$ 的长，记为 $d$，且

\[d = \frac{|(\overrightarrow{P_{1}P_{2}}, \boldsymbol{U}_{1}, \boldsymbol{U}_{2})|}{|\boldsymbol{U}_{1} \times \boldsymbol{U}_{2}|}. \tag{7.12}\]

（5）可建立异面直线公垂线的一般方程

\[\left\{ \begin{array}{l} (\overrightarrow{P_{1}P}, \boldsymbol{U}_{1}, \boldsymbol{U}_{1} \times \boldsymbol{U}_{2}) = 0, \\ (\overrightarrow{P_{2}P}, \boldsymbol{U}_{2}, \boldsymbol{U}_{1} \times \boldsymbol{U}_{2}) = 0. \end{array} \right. \tag{7.13}\]

（异面直线 $L_{1}, L_{2}$ 的公垂线既在过 $L_{1}$ 且平行于 $\boldsymbol{U}_{1} \times \boldsymbol{U}_{2}$ 的平面上，又在过 $L_{2}$ 且平行于 $\boldsymbol{U}_{1} \times \boldsymbol{U}_{2}$ 的平面上。）

例题

【例7.1】已知 $\boldsymbol{a}_1 = \{1,2,-3\},\boldsymbol{a}_2 = \{2,-3,x\},\boldsymbol{a}_3 = \{-2,x,6\}$。

（I）如 $\boldsymbol{a}_1 \perp \boldsymbol{a}_2$，则 $x =$ ______；
（Ⅱ）如 $\boldsymbol{a}_1 \parallel \boldsymbol{a}_3$，则 $x =$ ______；
（Ⅲ）如 $\boldsymbol{a}_1, \boldsymbol{a}_2, \boldsymbol{a}_3$ 共面，则 $x =$ ______。

【分析】（I）$\boldsymbol{a}_1 \perp \boldsymbol{a}_2 \Leftrightarrow \boldsymbol{a}_1 \cdot \boldsymbol{a}_2 = 0$，故 $1 \cdot 2 + 2 \cdot (-3) + (-3)x = 0$，得 $x = -\frac{4}{3}$。

（Ⅱ）$\boldsymbol{a}_1 \parallel \boldsymbol{a}_3 \Leftrightarrow \frac{x_1}{x_3} = \frac{y_1}{y_3} = \frac{z_1}{z_3}$ 故 $\frac{1}{-2} = \frac{2}{x} = \frac{-3}{6}$ 得 $x = -4$。
（Ⅲ）$\boldsymbol{a}_1, \boldsymbol{a}_2, \boldsymbol{a}_3$ 共面 $\Leftrightarrow (\boldsymbol{a}_1, \boldsymbol{a}_2, \boldsymbol{a}_3) = 0$，故 $\left| \begin{array}{ccc} 1 & 2 & -3 \\ 2 & -3 & x \\ -2 & x & 6 \end{array} \right| = 0$，得 $x = -4$ 或 $-6$。

【例7.2】直线 $L_{1}: \frac{x - 1}{1} = \frac{y - 5}{-2} = \frac{z + 8}{1}$ 与直线 $L_{2}: \left\{ \begin{array}{l}x - y = 6,\\ 2y + z = 3 \end{array} \right.$ 的夹角为 ______。

【分析】两条直线的夹角也就是这两条直线方向向量的夹角，$L_{1}$ 的方向向量 $\boldsymbol{S}_{1} = \{1, -2, 1\}$ 已知，对 $L_{2}$ 应通过方程转换化其为标准方程或参数方程来求 $L_{2}$ 的方向向量 $\boldsymbol{S}_{2}$。

令 $y = t$，直线 $L_{2}$ 的参数方程是 $\left\{ \begin{array}{l}x = t + 6,\\ y = t,\\ z = -2t + 3, \end{array} \right.$ 得到 $L_{2}$ 的方向向量

练习题

例题1

已知向量 $\boldsymbol{a} = \{2, -1, 3\}$，$\boldsymbol{b} = \{-1, 4, 2\}$，$\boldsymbol{c} = \{3, 0, -2\}$。
（I）计算 $\boldsymbol{a} + \boldsymbol{b}$ 和 $2\boldsymbol{a} - 3\boldsymbol{b}$。
（Ⅱ）求 $\boldsymbol{a} \cdot \boldsymbol{b}$ 和 $\boldsymbol{a} \times \boldsymbol{b}$。
（Ⅲ）判断 $\boldsymbol{a}$、$\boldsymbol{b}$、$\boldsymbol{c}$ 是否共面。

解答
（I）由向量加法公式：
$\boldsymbol{a} + \boldsymbol{b} = \{2 + (-1), -1 + 4, 3 + 2\} = \{1, 3, 5\}.$
由数乘和减法：
$2\boldsymbol{a} = \{4, -2, 6\},\quad 3\boldsymbol{b} = \{-3, 12, 6\},$
$2\boldsymbol{a} - 3\boldsymbol{b} = \{4 - (-3), -2 - 12, 6 - 6\} = \{7, -14, 0\}.$

（Ⅱ）数量积：
$\boldsymbol{a} \cdot \boldsymbol{b} = 2 \times (-1) + (-1) \times 4 + 3 \times 2 = -2 - 4 + 6 = 0.$
向量积：

\[\boldsymbol{i} & \boldsymbol{j} & \boldsymbol{k} \\ 2 & -1 & 3 \\ -1 & 4 & 2 \end{vmatrix} = \boldsymbol{i}(-1 \times 2 - 3 \times 4) - \boldsymbol{j}(2 \times 2 - 3 \times (-1)) + \boldsymbol{k}(2 \times 4 - (-1) \times (-1))$$ $$= \boldsymbol{i}(-2 - 12) - \boldsymbol{j}(4 + 3) + \boldsymbol{k}(8 - 1) = -14\boldsymbol{i} - 7\boldsymbol{j} + 7\boldsymbol{k} = \{-14, -7, 7\}.$$ （Ⅲ）计算混合积： $$(\boldsymbol{a}, \boldsymbol{b}, \boldsymbol{c}) = \begin{vmatrix} 2 & -1 & 3 \\ -1 & 4 & 2 \\ 3 & 0 & -2 \end{vmatrix} = 2 \times (4 \times (-2) - 2 \times 0) - (-1) \times ((-1) \times (-2) - 2 \times 3) + 3 \times ((-1) \times 0 - 4 \times 3)$$ $$= 2 \times (-8) + 1 \times (2 - 6) + 3 \times (0 - 12) = -16 - 4 - 36 = -56 \neq 0.$$ 混合积不为零，故 $\boldsymbol{a}$、$\boldsymbol{b}$、$\boldsymbol{c}$ 不共面。 --- ### 例题2 直线 $L_1$ 过点 $P_1(1, 2, -1)$，方向向量为 $\boldsymbol{S}_1 = \{2, -1, 3\}$；直线 $L_2$ 过点 $P_2(0, 1, 2)$，方向向量为 $\boldsymbol{S}_2 = \{1, 2, -1\}$。（I）求 $L_1$ 与 $L_2$ 的夹角。（Ⅱ）判断 $L_1$ 与 $L_2$ 是否异面，并求公垂线的长度。 **解答** （I）两直线的夹角即方向向量的夹角： $$\cos \theta = \frac{|\boldsymbol{S}_1 \cdot \boldsymbol{S}_2|}{|\boldsymbol{S}_1||\boldsymbol{S}_2|} = \frac{|2 \times 1 + (-1) \times 2 + 3 \times (-1)|}{\sqrt{2^2 + (-1)^2 + 3^2} \cdot \sqrt{1^2 + 2^2 + (-1)^2}} = \frac{|2 - 2 - 3|}{\sqrt{14} \cdot \sqrt{6}} = \frac{3}{\sqrt{84}} = \frac{\sqrt{21}}{14}.$$ 故夹角 $\theta = \arccos\left(\frac{\sqrt{21}}{14}\right)$。（Ⅱ）计算混合积： $$\overrightarrow{P_1P_2} = \{-1, -1, 3\},$$ $$(\overrightarrow{P_1P_2}, \boldsymbol{S}_1, \boldsymbol{S}_2) = \begin{vmatrix} -1 & -1 & 3 \\ 2 & -1 & 3 \\ 1 & 2 & -1 \end{vmatrix} = -1 \times ((-1) \times (-1) - 3 \times 2) - (-1) \times (2 \times (-1) - 3 \times 1) + 3 \times (2 \times 2 - (-1) \times 1)$$ $$= -1 \times (1 - 6) + 1 \times (-2 - 3) + 3 \times (4 + 1) = 5 - 5 + 15 = 15 \neq 0.$$ 混合积不为零，故 $L_1$ 与 $L_2$ 异面。公垂线长度： $$d = \frac{|(\overrightarrow{P_1P_2}, \boldsymbol{S}_1, \boldsymbol{S}_2)|}{|\boldsymbol{S}_1 \times \boldsymbol{S}_2|}.$$ 先求 $\boldsymbol{S}_1 \times \boldsymbol{S}_2$： $$\boldsymbol{S}_1 \times \boldsymbol{S}_2 = \begin{vmatrix} \boldsymbol{i} & \boldsymbol{j} & \boldsymbol{k} \\ 2 & -1 & 3 \\ 1 & 2 & -1 \end{vmatrix} = \boldsymbol{i}((-1) \times (-1) - 3 \times 2) - \boldsymbol{j}(2 \times (-1) - 3 \times 1) + \boldsymbol{k}(2 \times 2 - (-1) \times 1)$$ $$= \boldsymbol{i}(1 - 6) - \boldsymbol{j}(-2 - 3) + \boldsymbol{k}(4 + 1) = -5\boldsymbol{i} + 5\boldsymbol{j} + 5\boldsymbol{k} = \{-5, 5, 5\},$$ $$|\boldsymbol{S}_1 \times \boldsymbol{S}_2| = \sqrt{(-5)^2 + 5^2 + 5^2} = \sqrt{75} = 5\sqrt{3}.$$ 因此， $$d = \frac{15}{5\sqrt{3}} = \frac{3}{\sqrt{3}} = \sqrt{3}.$$ --- ### 例题3 已知向量 $\boldsymbol{a} = \{1, -2, 2\}$，$\boldsymbol{b} = \{3, 0, -4\}$。（I）求与 $\boldsymbol{a}$、$\boldsymbol{b}$ 都垂直的单位向量。（Ⅱ）求以 $\boldsymbol{a}$、$\boldsymbol{b}$ 为邻边的平行四边形的面积。 **解答** （I）与 $\boldsymbol{a}$、$\boldsymbol{b}$ 都垂直的向量为 $\boldsymbol{a} \times \boldsymbol{b}$： $$\boldsymbol{a} \times \boldsymbol{b} = \begin{vmatrix} \boldsymbol{i} & \boldsymbol{j} & \boldsymbol{k} \\ 1 & -2 & 2 \\ 3 & 0 & -4 \end{vmatrix} = \boldsymbol{i}((-2) \times (-4) - 2 \times 0) - \boldsymbol{j}(1 \times (-4) - 2 \times 3) + \boldsymbol{k}(1 \times 0 - (-2) \times 3)$$ $$= \boldsymbol{i}(8 - 0) - \boldsymbol{j}(-4 - 6) + \boldsymbol{k}(0 + 6) = 8\boldsymbol{i} + 10\boldsymbol{j} + 6\boldsymbol{k} = \{8, 10, 6\}.$$ 单位化： $$|\boldsymbol{a} \times \boldsymbol{b}| = \sqrt{8^2 + 10^2 + 6^2} = \sqrt{200} = 10\sqrt{2},$$ 单位向量为 $\pm \frac{1}{10\sqrt{2}}\{8, 10, 6\} = \pm \frac{1}{5\sqrt{2}}\{4, 5, 3\}$。（Ⅱ）平行四边形面积 $S = |\boldsymbol{a} \times \boldsymbol{b}| = 10\sqrt{2}$。\]