3

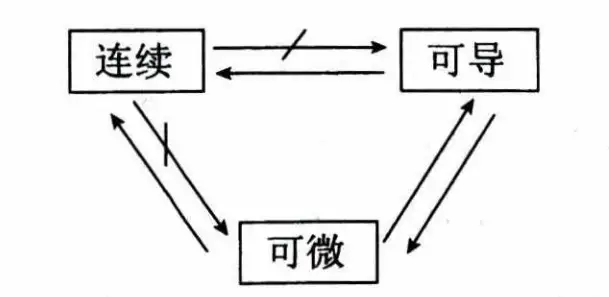
三、连续、可导、可微之间的关系

定理若函数 $y = f(x)$ 在点 $x_0$ 处可导，则 $f(x)$ 在点 $x_0$ 处连续.

(1) 反之不成立. 即若 $f(x)$ 在 $x_0$ 处连续，则 $f(x)$ 在 $x_0$ 处不一定可导.

(2) 不连续一定不可导. 若 $f(x)$ 在 $x_0$ 处不连续，则 $f(x)$ 在 $x_0$ 处一定不可导.

(3) 左、右导数均存在，则 $f(x)$ 在 $x_0$ 处连续.

定理函数 $y = f(x)$ 在点 $x_0$ 处可微的充分必要条件是 $f(x)$ 在 $x_0$ 处可导. 且 $dy = f'(x_0) dx$ .

(1) 可导 $\Leftrightarrow$ 可微.

(2) 可微一定连续，但连续不一定可微.

例 35

设函数 $f(x)=\begin{cases}x^2,&x\leqslant1,\\\quad ax+b,&x>1,\end{cases}$ 那么当 $a, b$ 取何值时， $f(x)$ 在 $x=1$ 处可导？

【解】 因可导必连续，由 $f(x)$ 在 $x=1$ 处可导，则 $f(x)$ 在 $x=1$ 处必连续。

$\lim_{x\to1^{-}}f(x)=\lim_{x\to1^{-}}x^2=1$ , $\lim_{x\to1^{+}}f(x)=\lim_{x\to1^{+}}(ax+b)=a+b$ , $f(1)=1$ ,

若要 $f(x)$ 在 $x=1$ 处连续，则 $\lim_{x\to1^{-}}f(x)=\lim_{x\to1^{+}}f(x)=f(1)$ ，即 $a+b=1$ 。

$f'_{-}(1)=\lim_{x\to1^{-}}\frac{f(x)-f(1)}{x-1}=\lim_{x\to1^{-}}\frac{x^2-1}{x-1}=\lim_{x\to1^{-}}(x+1)=2$ ,

$f'_{+}(1)=\lim_{x\to1^{+}}\frac{f(x)-f(1)}{x-1}=\lim_{x\to1^{+}}\frac{ax+b-1}{x-1}=\lim_{x\to1^{+}}\frac{ax-a}{x-1}=a$ ,

又 $f(x)$ 在 $x=1$ 点可导，则 $f'_{-}(1)=f'_{+}(1)$ ，即 $a=2$ ， $b=-1$ 。

所以，当 $a=2$ ， $b=-1$ 时， $f(x)$ 在 $x=1$ 处可导。

例 36

设函数 $f(x)=\begin{cases}\sin 2x+x^2\cos\frac{1}{x},&x\ne0,\\0,&x=0,\end{cases}$ 则 $f(x)$ 在 $x=0$ 处不成立的是

(A) 连续。 (B) 可导。 (C) 可微。 (D) 不可导。

【解】 由导数的定义知

$f'(0)=\lim_{x\to0}\frac{f(x)-f(0)}{x-0}=\lim_{x\to0}\frac{\sin 2x+x^2\cos\frac{1}{x}}{x}=\lim_{x\to0}\frac{\sin 2x}{x}+\lim_{x\to0}x\cos\frac{1}{x}=2$ ，

则 $f(x)$ 在 $x=0$ 处可导，从而 $f(x)$ 在 $x=0$ 处连续，可微。故应选 (D)。

例 37

试判断 $f(x)=\begin{cases}\frac{\sin|x|}{x},&x\ne0,\\1,&x=0\end{cases}$ 在 $x=0$ 处的连续性与可导性。

【解】 因 $\lim_{x\to0^-}f(x)=\lim_{x\to0^-}\frac{\sin(-x)}{x}=\lim_{x\to0^-}\frac{-x}{x}=-1$ ,

$\lim_{x\to0^+}f(x)=\lim_{x\to0^+}\frac{\sin x}{x}=1$ ，

又 $f(0)=1$ ，则 $f(x)$ 在 $x=0$ 处不连续，从而也不可导。

例 38

（2020，数一）设函数 $f(x)$ 在 $(-1,1)$ 上有定义，且 $\lim_{x\to0}f(x)=0$ ，则

(A) 当 $\lim_{x\to0}\frac{f(x)}{\sqrt{|x|}}=0$ 时， $f(x)$ 在 $x=0$ 处可导。

(B) 当 $\lim_{x\to0}\frac{f(x)}{x^2}=0$ 时， $f(x)$ 在 $x=0$ 处可导。

(D) 当 $f(x)$ 在 $x=0$ 处可导时， $\lim_{x\to0}\frac{f(x)}{x^2}=0$ 。

【解】可通过举反例说明 (A) (B) (D) 不正确。

例如取 $f(x)=\begin{cases}x^3,&x\ne0,\\1,&x=0,\end{cases}$ 则 $f(x)$ 在 $(-1,1)$ 内有定义，且 $\lim_{x\to0}f(x)=\lim_{x\to0}x^3=0$ ，

$\lim _{x \rightarrow 0} \frac{f(x)}{\sqrt{|x|}} = \lim _{x \rightarrow 0} \frac{x^{3}}{\sqrt{|x|}} = 0, \lim _{x \rightarrow 0} \frac{f(x)}{x^{2}} = \lim _{x \rightarrow 0} \frac{x^{3}}{x^{2}} = 0$ , 条件都满足,

但 $\lim _{x \rightarrow 0} f(x) = 0 \neq f(0)$ , 则 $f(x)$ 在 $x = 0$ 处不连续，从而在 $x = 0$ 处不可导。

因而 (A)(B) 都不正确。

取 $f(x) = x$ , 则 $\lim _{x \rightarrow 0} f(x) = 0, f(x)$ 在 $x = 0$ 处可导，但 $\lim _{x \rightarrow 0} \frac{f(x)}{x^{2}} = \lim _{x \rightarrow 0} \frac{x}{x^{2}} = \infty$ ，

因而 (D) 也不正确。

而选项 (C) 正确：由 $f(x)$ 在 $x = 0$ 处可导知 $f(x)$ 在 $x = 0$ 处连续，

则 $\lim _{x \rightarrow 0} f(x) = f(0) = 0$ ，从而

$\begin{aligned} \lim _{x \rightarrow 0} \frac{f(x)}{\sqrt{|x|}} & = \lim _{x \rightarrow 0} \frac{f(x) - f(0)}{x} \cdot \frac{x}{\sqrt{|x|}} = \lim _{x \rightarrow 0} \frac{f(x) - f(0)}{x - 0} \cdot \lim _{x \rightarrow 0} \frac{x}{\sqrt{|x|}} \\ & = f'(0) \cdot 0 = 0 . \end{aligned}$

所以 (C) 正确。故应选 (C)。